瓮安三中某班在2011年开展了一次“40公里长途拉练活动”,行进过程中,队伍始终保持一路纵队,到早上11点30分时,位于队尾的班主任请同样位于队尾的一位同学,跑步追赶位于队首的保安叔叔,并告诉他:“中午12点准时吃中餐,请您到时让队伍停下来,并选择一块较平的草地,以方便大家就餐.”然后以每秒比原来少1米的速度小跑回到队尾,这样,该同学跑完一个来回共用去了5分钟时间.已知队伍长315米,队伍行进的速度为5.4千米/时,求该同学追赶保安叔叔时的速度.
对于本题,我们给出了一种分析思路,请按要求认真阅读、填写,并解答出结果.
(1)由于原始数据单位不统一,第一步(化归单位):5分钟=______秒,5.4千米/时=______米/秒.
(2)若设该同学追赶保安叔叔时的速度为x米/秒,则用含x的代数式表示:他从队尾追到队首所用的时间为______秒,从队首返回队尾所用的时间为______秒.
(3)请根据以上分析解答本题.
解:(1)5分钟=300秒,5.4千米/时=1.5米/秒;
(2)设该同学追赶保安叔叔时的速度为x米/秒,他由队首返回队尾的速度为(x-1)m/s,
他从队尾追到队首所用的时间为:

,从队首返回队尾所用的时间为

秒;
(3)解:设该同学追赶队伍的速度为xm/s,则他由队首返回队尾的速度为(x-1)m/s,
5min=300s,5.4km/h=1.5m/s,
依题意有:

,
即:

,
解之得:x
1=0.1,x
2=3,
经检验:x
1=0.1和x
2=3都是原方程的根.
但当x=0.1时,x-1<0,故舍去.
答:设该同学追赶保安叔叔的速度为3m/s.
分析:(1)1分钟=60秒,1千米/时=
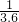
米/秒,由此换算即可;
(2)根据该同学的速度及队伍的速度,利用时间=路程÷速度即可得出答案;
(3)根据前面的分析,利用该同学跑完一个来回共用去了5分钟时间,可得出方程,解出即可.
点评:此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程,注意分式方程不要忘记检验.

 ,从队首返回队尾所用的时间为
,从队首返回队尾所用的时间为 秒;
秒; ,
, ,
,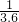 米/秒,由此换算即可;
米/秒,由此换算即可;

 名校课堂系列答案
名校课堂系列答案