
 如图,在等腰梯形ABCD中,上底AD=2,下底BC=8,M是腰AB的中点,若MD⊥CD,求梯形的面积.
如图,在等腰梯形ABCD中,上底AD=2,下底BC=8,M是腰AB的中点,若MD⊥CD,求梯形的面积. 分析 用作辅助线的方法把梯形的上底移到下底上,从而梯形的面积转化成三角形的面积来解决.
解答 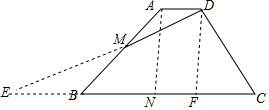 解:延长DM交CB的延长线于点E,
解:延长DM交CB的延长线于点E,
∵AD∥CE,∴∠ADM=∠E,
∵M是AB的中点,
∴AM=BM,
在△ADM与△BEM中,$\left\{\begin{array}{l}{∠ADM=∠BEM}\\{∠AND=∠BME}\\{AM=BM}\end{array}\right.$,
∴△ADM≌△BEM(ASA),
∴AD=BE.
∵AD=2,BC=8,
∴AD+BC=10,
∴EB+BC=10,即CE=20,过A作AN⊥BC于N,DF⊥BC于F,
则NF=AD=2,
∵AB=CD,
∴BN=CF=3,
∵DM⊥CD,DF⊥BC,
∴△DEF∽△CDF,
∴$\frac{CF}{DF}=\frac{DF}{EF}$,
∴DF2=3×7=21,
∴DF=$\sqrt{21}$,
∴S梯形ABCD=S△DCE=$\frac{1}{2}$×10×$\sqrt{21}$=5$\sqrt{21}$.
点评 本题考查的是梯形和解直角三角形,需要用到梯形的面积转化成三角形的面积.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
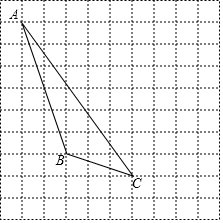 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.2217×106 | B. | 0.2217×107 | C. | 2.217×106 | D. | 2.217×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11×104 | B. | 1.1×105 | C. | 1.1×104 | D. | 0.11×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 事件A和事件B都是必然事件 | |
| B. | 事件A是随机事件,事件B是不可能事件 | |
| C. | 事件A是必然事件,事件B是随机事件 | |
| D. | 事件A和事件B都是随机事件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com