
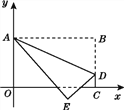
【题目】如图,将长方形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将长方形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,点B的坐标为_________,点E的坐标为_________;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
【答案】(1)(3,4),(0,1);(2)点E能恰好落在x轴上,理由见解析.
【解析】试题分析:(1)根据点A、点D、点C的坐标和矩形的性质可以得到点B和点E的坐标;
(2)由折叠的性质求得线段DE和AE的长,然后利用勾股定理得到有关m的方程,求得m的值即可.
试题解析:(1)点B的坐标为(3,4),
∵AB=BD=3,
∴△ABD是等腰直角三角形,
∴∠BAD=45°,
则∠DAE=∠BAD=45°,
则E在y轴上.
AE=AB=BD=3,
∴四边形ABDE是正方形,OE=1,
则点E的坐标为(0,1);
(2)点E能恰好落在x轴上.理由如下:
∵四边形OABC为矩形,
∴BC=OA=4,∠AOC=∠DCE=90°,
由折叠的性质可得:DE=BD=OA-CD=4-1=3,AE=AB=OC=m,
假设点E恰好落在x轴上,在Rt△CDE中,由勾股定理可得EC=![]()
则有OE=OC-CE=m-2![]()
在Rt△AOE中,OA2+OE2=AE2
即42+(m-2![]() )2=m2
)2=m2
解得m=3![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)抛物线![]() 经过点A (4,0),点B (1,-3) ,求该抛物线的解析式;
经过点A (4,0),点B (1,-3) ,求该抛物线的解析式;
(2)如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?

(3)如图,点P![]() (
(![]() >0),在
>0),在![]() 轴正半轴上,过点P作平行于
轴正半轴上,过点P作平行于![]() 轴的直线,分别交抛物线
轴的直线,分别交抛物线![]() 于点A,B,交抛物线
于点A,B,交抛物线![]() 于点C,D,求
于点C,D,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=-x-2交x轴于点A,交y轴于点B,抛物线y2=ax2+bx+c的顶点为A,且经过点B.
(1)求该抛物线的解析式;
(2)求当y1≥y2时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图①,在△ABC中,∠ACB=2∠B,AD为∠BAC的角平分线,
求证:AB=AC+CD
小明同学经过思考,得到如下解题思路:
在AB上截取AE=AC,连接DE,得到△ADE≌△ADC,从而易证AB=AC+CD
(1)请你根据以上解思路写出证明过程;
(2)如图②,若AD为△ABC的外角∠CAE平分线,交BC的延长线于点D,
∠D=25°,其他条件不变,求∠B的度数。


查看答案和解析>>
科目:初中数学 来源: 题型:
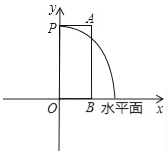
【题目】某市人民广场上要建一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米.
(1)求这条抛物线的解析式;
(2)若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件:
①在足球赛中,弱队战胜强队.
②抛掷1枚硬币,硬币落地时正面朝上.
③任取两个正整数,其和大于1
④长为3cm,5cm,9cm的三条线段能围成一个三角形.
其中确定事件有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com