
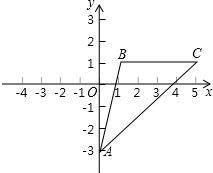
 在平面直角坐标系中,已知点A(0,-3),点B(m,1),C(m+4,1);
在平面直角坐标系中,已知点A(0,-3),点B(m,1),C(m+4,1);分析 (1)由题意得出BC∥x轴,BC=4,△ABC中BC边上的高=4,即可求出△ABC的面积;
(2)由题意得出m<0,B在第二象限,则BD=-m,CD=4+m,PD=1-m,由射影定理得出方程,由△<0,得出方程2m2+2m+1=0无实数根,即可得出结论;
(3)作QM⊥BC于M,由垂径定理得出BM=CM=$\frac{1}{2}$BC=2,由切线的性质得出QM=4-R,由勾股定理得出方程,解方程即可;
(4)当∠BAC最大时,sin∠BAC的值最大,此时y轴是BC的垂直平分线,则BD=CD=$\frac{1}{2}$BC=2,AD=4,由勾股定理求出AB=AC=2$\sqrt{5}$,作BN⊥AC与N,由△ABC的面积求出BN,再由三角函数即可得出sin∠BAC的最大值.
解答 解:(1)∵A(0,-3),点B(m,1),C(m+4,1),
∴BC∥x轴,BC=4,△ABC中BC边上的高=1+3=4,
∴ △ABC的面积=$\frac{1}{2}$×4×4=8;
△ABC的面积=$\frac{1}{2}$×4×4=8;
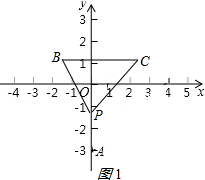
(2)若点P(0,m)在x轴下方,不存在m使得∠BPC=90°;理由如下:
∵点P(0,m)在x轴下方,
∴m<0,则B在第二象限,如图1所示:
则BD=-m,CD=4+m,PD=1-m,
∵BC∥x轴,
∴∠CDP=90°,
若∠BPC=90°,由射影定理得:PD2=BD•CD,
即(1-m)2=-m(4-m),
整理得:2m2+2m+1=0,
∵△=22-4×2×1<0,
∴方程2m2+2m+1=0无实数根,
∴若点P(0,m)在x轴下方,不存在m使得∠BPC=90°;
(3)若⊙Q过点B、C且与过A平行于x轴的直线相切,如图2所示:
作QM⊥BC于M,则BM=CM=$\frac{1}{2}$BC=2,
设⊙Q的半径为R,则QM=4-R,BQ=R,
由勾股定理得:BM2+(4-R)2=R2,
解得:R=$\frac{5}{2}$,
即⊙Q的半径为$\frac{5}{2}$;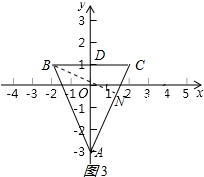
(4)sin∠BAC的最大值为$\frac{4}{5}$;理由如下:
当∠BAC最大时,sin∠BAC的值最大,此时y轴是BC的垂直平分线,如图3所示:
则BD=CD=$\frac{1}{2}$BC=2,AD=1+3=4,AB=AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
作BN⊥AC与N,
∵△ABC的面积=$\frac{1}{2}$AC•BN=8,
即$\frac{1}{2}$×2$\sqrt{5}$×BN=8,
解得:BN=$\frac{8\sqrt{5}}{5}$,
∴sjn∠BAC=$\frac{BN}{AB}$=$\frac{\frac{8\sqrt{5}}{5}}{2\sqrt{5}}$=$\frac{4}{5}$,
即sin∠BAC的最大值为$\frac{4}{5}$.
点评 本题是圆的综合题目,考查了垂径定理、切线的性质、勾股定理、射影定理、一元二次方程根的判别式、三角形面积的计算以及三角函数等知识;本题综合性强,有一定难度,需要通过作辅助线运用垂径定理和勾股定理才能得出结果.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
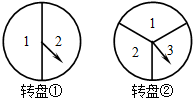 某班举行联欢会,规定每个同学同时转动转盘①与转盘②(它们分别被二等分和三等分).若两个转盘停止后,指针所指的数字之积为奇数,则这个同学要表演唱歌节目;若数字之积为偶数,则要表演其它节目.试求出转动转盘的同学表演唱歌节目的概率.(用树状图或列表方法求解)
某班举行联欢会,规定每个同学同时转动转盘①与转盘②(它们分别被二等分和三等分).若两个转盘停止后,指针所指的数字之积为奇数,则这个同学要表演唱歌节目;若数字之积为偶数,则要表演其它节目.试求出转动转盘的同学表演唱歌节目的概率.(用树状图或列表方法求解)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0),B(4,0)两点,与y轴交于点C.
如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0),B(4,0)两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com