
 ��ͼ���Գ�����OABC�Ķ���OΪԭ�㣬OA����ֱ��Ϊx�ᣬOC����ֱ��Ϊy�ᣬ����ƽ��ֱ������ϵ����֪OA=3��OC=2����E��AB���е㣬��OA��ȡһ��D������BD����A����BD�ĶԳƵ�ǡ�������߶�BC���ϵĵ�F����
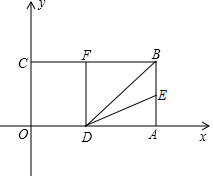
��ͼ���Գ�����OABC�Ķ���OΪԭ�㣬OA����ֱ��Ϊx�ᣬOC����ֱ��Ϊy�ᣬ����ƽ��ֱ������ϵ����֪OA=3��OC=2����E��AB���е㣬��OA��ȡһ��D������BD����A����BD�ĶԳƵ�ǡ�������߶�BC���ϵĵ�F�������� ��1����BDA��BD���ۣ�ʹ��A����BC���ϵĵ�F��������֪���ı���ADFB�������Σ����BF=AB=OC=2����CF=3-2=1�����E��F������Ϳ��������
��2����ƽ������ϵ�������ľ��빫ʽ���ɵó��߶Σ��ٷ���������ñ���Ƚ���������⼴�ɵó����ۣ�
��3������E����x��ĶԳƵ�E�䣬����F����y��ĶԳƵ�F�䣬����E��F�䣬�ֱ���x�ᡢy�ύ�ڵ�M��N�����M��N��������㣮����߶�E��F��ij��ȣ������ı���MNFE���ܳ�����Сֵ��
��� �⣺��1����OC=2���ı���OABC�Ǿ��Σ�
��AB=OC=2��
�ߵ�E��AB���е㣬
��AE=1��
��AO=3��
��E��3��1����
�����۵��ɵ�DA=DF��
��DF=CO=2��
��AD=2��
��DO=3-2=1��
��F��1��2����
��2�����ڣ�
���ɣ�
�ɣ�1��֪��E��3��1����O��0��0��
��P��a��2����0��a��3����
��PE=$\sqrt{��a-3��^{2}+1}$��PO=$\sqrt{{a}^{2}+4}$��EO=$\sqrt{10}$��
�ߡ�OEPΪ���������Σ�
��ٵ�PE=POʱ����$\sqrt{��a-3��^{2}+1}$=$\sqrt{{a}^{2}+4}$��
��a=1��
��P��1��2����
�ڵ�PE=EOʱ����$\sqrt{��a-3��^{2}+1}$=$\sqrt{10}$��
��a=0��a=6���ᣩ��
��P��0��2����
�۵�PO=EOʱ����$\sqrt{{a}^{2}+4}$=$\sqrt{10}$��
��a=$\sqrt{6}$��a=-$\sqrt{6}$���ᣩ��
��P��$\sqrt{6}$��2����
�������������ĵ�P������Ϊ��1��2����0��2����$\sqrt{6}$��2����
��3����ͼ2��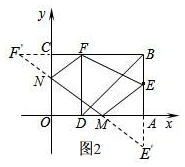
����E����x��ĶԳƵ�E�䣬
����F����y��ĶԳƵ�F�䣬����E��F�䣬�ֱ�
��x�ᡢy�ύ�ڵ�M��N������FN��NM��ME��
��ʱ�ı���MNFE���ܳ���С��
��E�䣨3��-1����F�䣨-1��2����
��ֱ��E��F��Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{3k+b=-1}\\{-k+b=2}\end{array}\right.$��
����������飬��$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{5}{4}}\end{array}\right.$��
��ֱ��E��F��Ľ���ʽΪy=-$\frac{3}{4}$x+$\frac{5}{4}$��
��y=0ʱ��x=$\frac{5}{3}$��
��M���������$\frac{5}{3}$��0����
��x=0ʱ��y=$\frac{5}{4}$��
��N���������0��$\frac{5}{4}$����
��E��E�����x��Գƣ�F��F�����y��Գƣ�
��NF=NF�䣬ME=ME�䣮F��B=4��E��B=3��
��Rt��BE��F����F'E'=$\sqrt{F'{B}^{2}+E'{B}^{2}}$=5��
��FN+NM+ME=F��N+NM+ME��=F��E��=5��
��Rt��BEF��EF=$\sqrt{B{E}^{2}+B{F}^{2}}$=$\sqrt{5}$��
��FN+NM+ME+EF=F'E'+EF=5+$\sqrt{5}$��
���ı���MNFE���ܳ���Сֵ��5+$\sqrt{5}$��
���� �������ı����ۺ��⣬��Ҫ�����˴���ϵ������������ʽ�����ɶ��������������ε����ʣ����߶εĺ���С����������Ľ��˼·�Ǹ��ݶԳ�ת��Ϊ����֮��ľ�������⣮


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��2 | B�� | a��2 | C�� | a��1 | D�� | a��1��a��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
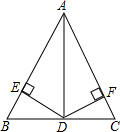 ��֪����ͼ����ABC�У�ADƽ�֡�BAC����BD=CD��DE��AB��DF��AC������ֱ�ΪE��F����֤��EB=FC��
��֪����ͼ����ABC�У�ADƽ�֡�BAC����BD=CD��DE��AB��DF��AC������ֱ�ΪE��F����֤��EB=FC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD��BEFG��Ϊ�����Σ�
��ͼ���ı���ABCD��BEFG��Ϊ�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
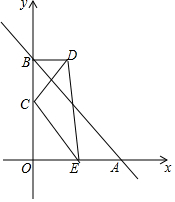 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��0��4������E��2��0����OA�ϣ���C������Ϊ��0��m����m��4������C����AB�ĶԳƵ��ǵ�D������BD��CD��CE��DE
��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��0��4������E��2��0����OA�ϣ���C������Ϊ��0��m����m��4������C����AB�ĶԳƵ��ǵ�D������BD��CD��CE��DE�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���ACB=90�㣬AC=8��BC=6��P��ֱ��AB�ϵĶ��㣨�����B�غϣ�������BCP��CP���ڵ�ֱ�߷��ۣ��õ���B��CP������B��A��B��A���ȵ���Сֵ��m��B��A���ȵ����ֵ��n����m+n��ֵ����16��
��ͼ���ڡ�ABC�У���ACB=90�㣬AC=8��BC=6��P��ֱ��AB�ϵĶ��㣨�����B�غϣ�������BCP��CP���ڵ�ֱ�߷��ۣ��õ���B��CP������B��A��B��A���ȵ���Сֵ��m��B��A���ȵ����ֵ��n����m+n��ֵ����16���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������ֽƬABC�У���BCA=90�㣬��AC��ȡһ��E����BEΪ�ۺ۽��з��ۣ�ʹAB��һ������BC�غϣ�A��BC�ӳ����ϵĵ�D�غϣ�����A=30�㣬AC=6����DE�ij���Ϊ��������
��ͼ��������ֽƬABC�У���BCA=90�㣬��AC��ȡһ��E����BEΪ�ۺ۽��з��ۣ�ʹAB��һ������BC�غϣ�A��BC�ӳ����ϵĵ�D�غϣ�����A=30�㣬AC=6����DE�ij���Ϊ��������| A�� | 6 | B�� | 4 | C�� | 3 | D�� | 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com