
如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)求点N落在BD上时t的值;
(2)直接写出点O在正方形PQMN内部时t的取值范围;
(3)当点P在折线AD﹣DO上运动时,求S与t之间的函数关系式;
(4)直接写出直线DN平分△BCD面积时t的值.

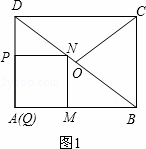
解:(1)当点N落在BD上时,如图1.
∵四边形PQMN是正方形,
∴PN∥QM,PN=PQ=t.
∴△DPN∽△DQB.
∴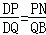 .
.
∵PN=PQ=PA=t,DP=3﹣t,QB=AB=4,
∴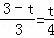 .
.
∴t=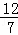 .
.
∴当t=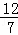 时,点N落在BD上.
时,点N落在BD上.
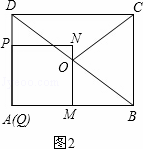
(2)①如图2,
则有QM=QP=t,MB=4﹣t.
∵四边形PQMN是正方形,
∴MN∥DQ.
∵点O是DB的中点,
∴QM=BM.
∴t=4﹣t.
∴t=2.
②如图3,
∵四边形ABCD是矩形,
∴∠A=90°.
∵AB=4,AD=3,
∴DB=5.
∵点O是DB的中点,
∴DO=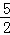 .
.
∴1×t=AD+DO=3+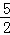 .
.
∴t=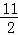 .
.
∴当点O在正方形PQMN内部时,t的范围是2<t<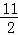 .
.
(3)①当0<t≤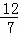 时,如图4.
时,如图4.
S=S正方形PQMN=PQ2=PA2=t2.
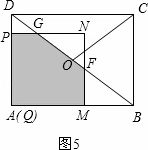
②当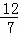 <t≤3时,如图5,
<t≤3时,如图5,
∵tan∠ADB=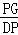 =
=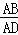 ,
,
∴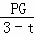 =
=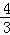 .
.
∴PG=4﹣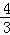 t.
t.
∴GN=PN﹣PG=t﹣(4﹣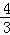 t)=
t)=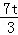 ﹣4.
﹣4.
∵tan∠NFG=tan∠ADB=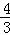 ,
,
∴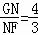 .
.
∴NF=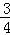 GN=
GN=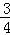 (
(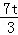 ﹣4)=
﹣4)=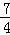 t﹣3.
t﹣3.
∴S=S正方形PQMN﹣S△GNF
=t2﹣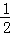 ×(
×(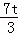 ﹣4)×(
﹣4)×(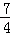 t﹣3)
t﹣3)
=﹣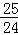 t2+7t﹣6.
t2+7t﹣6.
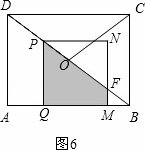
③当3<t≤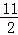 时,如图6,
时,如图6,
∵四边形PQMN是正方形,四边形ABCD是矩形.
∴∠PQM=∠DAB=90°.
∴PQ∥AD.
∴△BQP∽△BAD.
∴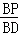 =
=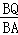 =
=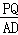 .
.
∵BP=8﹣t,BD=5,BA=4,AD=3,
∴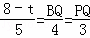 .
.
∴BQ=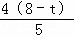 ,PQ=
,PQ=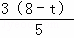 .
.
∴QM=PQ=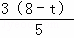 .
.
∴BM=BQ﹣QM=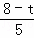 .
.
∵tan∠ABD= ,
,
∴FM=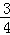 BM=
BM=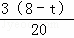 .
.
∴S=S梯形PQMF=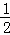 (PQ+FM)•QM
(PQ+FM)•QM
=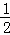 [
[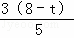 +
+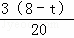 ]•
]•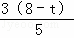
=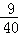 (8﹣t)2
(8﹣t)2
=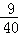 t2﹣
t2﹣ t+
t+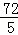 .
.
综上所述:当0<t≤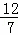 时,S=t2.
时,S=t2.
当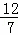 <t≤3时,S=﹣
<t≤3时,S=﹣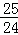 t2+7t﹣6.
t2+7t﹣6.
当3<t≤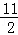 时,S=
时,S=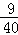 t2﹣
t2﹣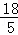 t+
t+ .
.
(4)设直线DN与BC交于点E,
∵直线DN平分△BCD面积,
∴BE=CE=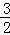 .
.
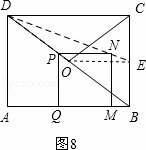
①点P在AD上,过点E作EH∥PN交AD于点H,如图7,
则有△DPN∽△DHE.
∴ .
.
∵PN=PA=t,DP=3﹣t,DH=CE=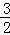 ,EH=AB=4,
,EH=AB=4,
∴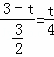 .
.
解得;t=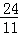 .
.
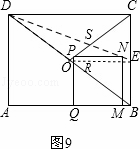
②点P在DO上,连接OE,如图8,
则有OE=2,OE∥DC∥AB∥PN.
∴△DPN∽△DOE.
∴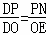 .
.
∵DP=t﹣3,DO=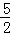 ,OE=2,
,OE=2,
∴PN=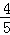 (t﹣3).
(t﹣3).
∵PQ=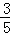 (8﹣t),PN=PQ,
(8﹣t),PN=PQ,
∴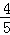 (t﹣3)=
(t﹣3)=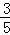 (8﹣t).
(8﹣t).
解得:t=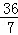 .
.
③点P在OC上,设DE与OC交于点S,连接OE,交PQ于点R,如图9,
则有OE=2,OE∥DC.
∴△DSC∽△ESO.
∴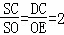 .
.
∴SC=2SO.
∵OC=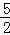 ,
,
∴SO=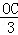 =
=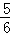 .
.
∵PN∥AB∥DC∥OE,
∴△SPN∽△SOE.
∴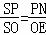 .
.
∵SP=3+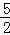 +
+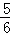 ﹣t=
﹣t=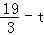 ,SO=
,SO=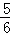 ,OE=2,
,OE=2,
∴PN=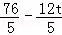 .
.
∵PR∥MN∥BC,
∴△ORP∽△OEC.
∴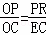 .
.
∵OP=t﹣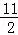 ,OC=
,OC=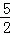 ,EC=
,EC=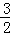 ,
,
∴PR= .
.
∵QR=BE=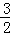 ,
,
∴PQ=PR+QR=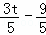 .
.
∵PN=PQ,
∴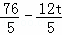 =
=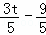 .
.
解得:t=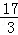 .
.
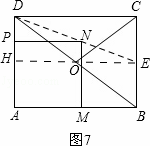
综上所述:当直线DN平分△BCD面积时,t的值为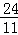 、
、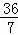 、
、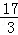 .
.




科目:初中数学 来源: 题型:
下列命题是假命题的是( )
|
| A. | 不在同一直线上的三点确定一个圆 |
|
| B. | 矩形的对角线互相垂直且平分 |
|
| C. | 正六边形的内角和是720° |
|
| D. | 角平分线上的点到角两边的距离相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件中,必然事件是
A. 抛掷一枚硬币,正面朝上
B. 打开电视,正在播放广告
C. 体育课上,小刚跑完1000米所用时间为1分钟
D. 袋中只有4个球,且都是红球,任意摸出一球是红球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com