练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如下图，直线过正方形ABCD的顶点B，点A、C到直线的距离分别是1和2，则正方形的边长是               。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：新教材完全解读　九年级数学　下册(配北师大版新课标) 北师大版新课标 题型：044

    如下图所示，在直角坐标系中，正方形ABOD的边长为a，O为原点，点B在x轴的负半轴上，点D在y轴的正半轴上，直线OE的解析式为y＝2x，直线CF过x轴上一点C(－a，0)，且与OE平行．现正方形以每秒的速度匀速沿x轴正方向平行移动，设运动时间为t秒，正方形被夹在直线OE，OF间的部分的面积为S．

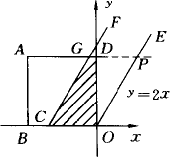
    (1)当0≤t＜4时，写出S与t的函数关系；

    (2)当4≤t≤5时，写出S与t的函数关系，在这个范围内，S有无最大值？若有，请求出最大值；若没有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2006年初中数学总复习下册 题型：044

    我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分．

    探索下列问题：

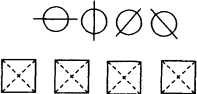
    (1)在下图给出的四个正方形中，各画出一条直线(依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线)，将每个正方形都分割成面积相等的两部分；

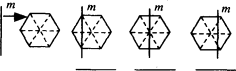
    (2)一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．

    ①请你在下图中相应图形下方的横线上分别填写S1与S2的数量关系式(用“＜”，“＝”，“＞”连接)．

    ②请你在下图中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“＜”，“＝”，“＞”连接)．

    (3)是否存在一条直线，将一个任意的平面图形(如下图)分割成面积相等的两部分，请简略说出理由．

    查看答案和解析>>

    科目：初中数学 来源：2007年江苏地区数学中考动态型试题－新人教 题型：059

    如下图，在边长为2个单位长度的正方形ABCD中，点O、E分别是AD、AB的中点，点F是以点O为圆心、OE的长为半径的圆弧与DC的交点，点P是上的动点，连结OP，并延长交直线BC于点K．

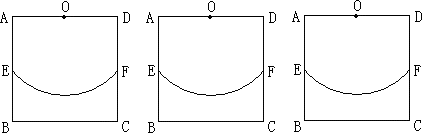
    (1)当点P从点E沿运动到点F时，点K运动了多少个单位长度？

    (2)过点P作所在圆的切线，当该切线不与BC平行时，设它与射线AB、直线BC分别交于点M、G．

    ①当K与B重合时，BG∶BM的值是多少？

    ②在点P运动的过程中，是否存在BG∶BM＝3的情况？你若认为存在，请求出BK的值；你若认为不存在，试说明其中的理由．

    一般地，是否存在BG∶BM＝n(n为正整数)的情况？试提出你的猜想(不要求证明)．

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：证明题

    已知如下图，过正方形ABCD的顶点A作对角线BD的平行线，在这条直线上取点E，使BE=BD，且BE与AD交于点F。求证：DE=DF。

    查看答案和解析>>

    同步练习册答案