
【题目】如图,已知,在平面直角坐标系中,A(﹣3,﹣4),B(0,﹣2).
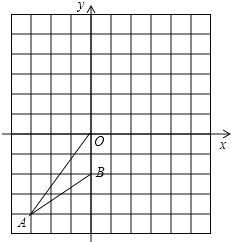
(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1,B1的坐标;
(2)判断以A,B,A1,B1为顶点的四边形的形状,并说明理由.
【答案】(1)A1(3,4),B1(0,2);(2)平行四边形,理由见试题解析
【解析】
试题分析:(1)由于△OAB绕O点旋转180°得到△OA1B1,利用关于原点中心对称的点的坐标特征得到A1,B1的坐标,然后描点,再连结OB1、OA1和A1B1即可;
(2)根据中心对称的性质得OA=OA1,OB=OB1,则利用对角线互相平分得四边形为平行四边形可判断四边形ABA1B1为平行四边形.
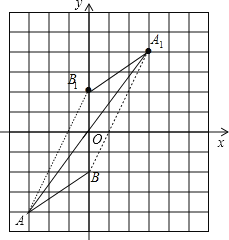
试题解析:(1)如图,A1(3,4),B1(0,2);
(2)以A,B,A1,B1为顶点的四边形为平行四边形,理由如下:
∵△OAB绕O点旋转180°得到△OA1B1,
∴点A与点A1关于原点对称,点B与点B1关于原点对称,
∴OA=OA1,OB=OB1,
∴四边形ABA1B1为平行四边形.


科目:初中数学 来源: 题型:
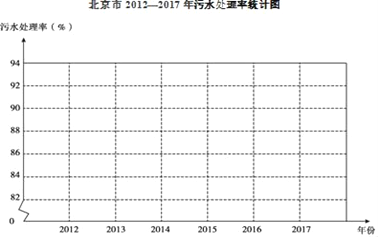
【题目】北京市积极开展城市环境建设,其中污水治理是重点工作之一,以下是北京市2012﹣2017年污水处理率统计表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
污水处理率(%) | 83.0 | 84.6 | 86.1 | 87.9 | 90.0 | 92.0 |
(1)用折线图将2012﹣2017年北京市污水处理率表示出来,并在图中标明相应的数据;
(2)根据统计图表中提供的信息,预估2018年北京市污水处理率约为_____%,说明你的预估理由:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完三角形的高后,小明对三角形与高线做了如下研究:如图,![]() 是
是![]() 中边
中边![]() 上的-点,过点
上的-点,过点![]() 、
、![]() 分别作、
分别作、![]() 、
、![]() 、
、![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() 、
、![]() ,由
,由![]() 与
与![]() 的面积之和等于
的面积之和等于![]() 的面积,有等量关系式:
的面积,有等量关系式:![]() .像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式,从而用于解决数学问题的方法称为“等积法”,下面请尝试用这种方法解决下列问题.
.像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式,从而用于解决数学问题的方法称为“等积法”,下面请尝试用这种方法解决下列问题.



图(1) 图(2)
(1)如图(1), 矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,过点
上一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,求
,求![]() 的值;
的值;
(2)如图(2),在![]() 中,角平分线
中,角平分线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 分别作
分别作![]() 、
、![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC外作等腰三角形ABD和等腰三角形ACE,且∠BAD=∠CAE=90°,AM为△ABC中BC边上的中线,连接DE.求证:DE=2AM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点![]() ,
,![]() 表示的数
表示的数![]() ,
,![]() 满足
满足![]() ,点
,点![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),
重合),![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 同时向数轴正方向移动,点
同时向数轴正方向移动,点![]() 运动速度为每秒2个单位长度,点
运动速度为每秒2个单位长度,点![]() 运动速度为每秒3个单位长度,设运动时间为
运动速度为每秒3个单位长度,设运动时间为![]() 秒(
秒(![]() ).
).
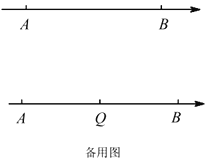
(1)直接写出![]() ______,
______,![]() ______;
______;
(2)若![]() 点表示的数是0.
点表示的数是0.
①![]() ,则
,则![]() 的长为______(直接写出结果);
的长为______(直接写出结果);
②点![]() ,
,![]() 在移动过程中,线段
在移动过程中,线段![]() ,
,![]() 之间是否存在某种确定的数量关系,判断并说明理由;
之间是否存在某种确定的数量关系,判断并说明理由;
(3)点![]() ,
,![]() 均在线段
均在线段![]() 上移动,若
上移动,若![]() ,且
,且![]() 到线段
到线段![]() 的中点
的中点![]() 的距离为3,请求出符合条件的点
的距离为3,请求出符合条件的点![]() 表示的数.
表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ
cos(α+β)=cosαcosβ﹣sinαsinβ,cos(α﹣β)=cosαcosβ+sinαsinβ
tan(α+β)=![]() (1﹣tanαtanβ≠0)
(1﹣tanαtanβ≠0)
tan(α﹣β)=![]() (1+tanαtanβ≠0)
(1+tanαtanβ≠0)
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
如:tan105°=tan(45°+60°)=![]()
根据上面的知识,你可以选择适当的公式解决下面问题:
如图,两座建筑物AB和DC的水平距离BC为24米,从点A测得点D的俯角α=15°,测得点C的俯角β=75°,求建筑物CD的高度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com