
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

【答案】(1)证明见解析;(2)点P、Q在运动的过程中,∠QMC不变.理由见解析.(3)不变,理由见解析.
【解析】试题分析:(1)、根据等边三角形可得∠ABQ=∠CAP,AB=CA,根据速度相同可得AP=BQ,从而得出三角形全等;(2)、根据△ABQ≌△CAP得出∠BAQ=∠ACP,然后根据∠QMC=∠BAQ+∠MAC得出答案;(3)、根据△ABQ≌△CAP得出∠BAQ=∠ACP,然后根据∠QMC=∠BAQ+∠MAC得出答案.
试题解析:(1)、∵△ABC是等边三角形 ∴∠ABQ=∠CAP,AB=CA, 又∵点P、Q运动速度相同,
∴AP=BQ, 在△ABQ与△CAP中,AB=AC,∠ABQ=∠CAP,AP=BQ ∴△ABQ≌△CAP(SAS);
(2)、点P、Q在运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP, ∴∠BAQ=∠ACP, ∵∠QMC=∠ACP+∠MAC, ∴∠QMC=∠BAQ+∠MAC=∠BAC=60°
(3)、点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变.
理由:∵△ABQ≌△CAP, ∴∠BAQ=∠ACP, ∵∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°


科目:初中数学 来源: 题型:
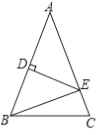
【题目】如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】((2016甘肃省兰州市)对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:![]() 交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
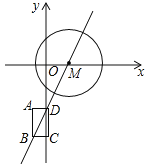
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校举办的足球比赛中,规定:胜一场得3分,平一场得1分,负一场得0分.某班足球队参加了12场比赛,共得22分,已知这个球队只输了2场,那么此队胜几场,平几场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】((2016江西省)如图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为“叠弦角”,△AOP为“叠弦三角形”.
【探究证明】
(1)请在图1和图2中选择其中一个证明:“叠弦三角形”(△AOP)是等边三角形;
(2)如图2,求证:∠OAB=∠OAE′.
【归纳猜想】
(3)图1、图2中的“叠弦角”的度数分别为 , ;
(4)图n中,“叠弦三角形” 等边三角形(填“是”或“不是”)
(5)图n中,“叠弦角”的度数为 (用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】((2016北京市)在平面直角坐标系xOy中,点P的坐标为(![]() ,
,![]() ),点Q的坐标为(
),点Q的坐标为(![]() ,
,![]() ),且
),且![]() ,
,![]() ,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
(1)已知点A的坐标为(1,0).
①若点B的坐标为(3,1)求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为![]() ,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
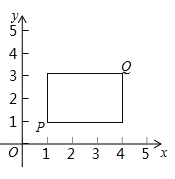
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com