
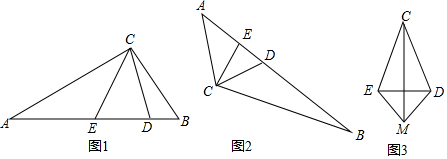
分析 (1)先用等腰三角形的性质和三角形的内角和得出,∠ACD=$\frac{1}{2}$(180°-∠A),∠BCE=$\frac{1}{2}$(180°-∠B)进而得出90°+$\frac{1}{2}$∠ACB-∠DCE=∠ACB即:∠DCE=90°-$\frac{1}{2}$∠ACB=45°;
(2)同(1)的方法得出结论即可;
(3)先利用对称性得出CP=CQ,∠PCE+∠QCD=45°,由于点M关于CE,CD对称点均在直线ED上,即可得出∠CPQ=∠CQP=45°,进而判断出△CPE≌△CQD即可得出CM是DE的垂直平分线上即可得出结论.
解答 解:(1)∵AD=AC,BC=BE,
∴∠ACD=∠ADC,∠BCE=∠BEC,
∴∠ACD=$\frac{1}{2}$(180°-∠A)
∠BCE=$\frac{1}{2}$(180°-∠B)
∴∠ACD+∠BCE-∠DCE=180°-$\frac{1}{2}$(∠A+∠B)-∠DCE=180°-$\frac{1}{2}$(180°-∠ACB)-∠DCE=90°+$\frac{1}{2}$∠ACB-∠DCE=∠ACB,
∴∠DCE=90°-$\frac{1}{2}$∠ACB=45°.
(2)∵AD=AC,BC=BE,
∴∠ACD=∠ADC,∠BCE=∠BEC,
∴∠ACD=$\frac{1}{2}$(180°-∠A)
∠BCE=$\frac{1}{2}$(180°-∠B)
∴∠ACD+∠BCE-∠DCE=180°-$\frac{1}{2}$(∠A+∠B)-∠DCE=180°-$\frac{1}{2}$(180°-∠ACB)-∠DCE=90°+$\frac{1}{2}$∠ACB-∠DCE=∠ACB,
∴∠DCE=90°-$\frac{1}{2}$∠ACB=90°-$\frac{1}{2}α$.
(3)△EDM等腰三角形,
理由:如图3,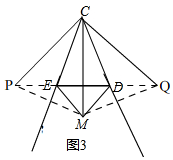 作出点M关于CE的对称点P,
作出点M关于CE的对称点P,
∴∠PCE=∠MCE,CP=CM.
作出点M关于CD的对称点Q,
∴∠QCD=∠MCD,CQ=CM,
∴CP=CQ,
由(1)知,∠DCE=45°,
∴∠PCE+∠QCD=∠MCE+∠MCD=45°,
∴∠PCQ=∠PCE+∠DCE+∠QCD=90°,
∵点M关于CE,CD对称点均在直线ED上,
∴∠CPQ=∠CQP=45°,
∴点P,E,D,Q在同一条直线上,
∵CE=CD,
∴∠CED=∠CDE,
∴∠CEP=∠CDQ,
在△CPE和△CQD中,$\left\{\begin{array}{l}{∠CPQ=∠CQP=45°}\\{∠CEP=∠CDQ}\\{CE=CD}\end{array}\right.$,
∴△CPE≌△CQD,
∴∠PCE=∠QCD,
∴∠PCE=∠MCE=∠DCM=∠QCD,
∴∠ECM=∠DCM,
∵CE=CD,
∴CM垂直平分ED,
∴ME=MD,
∴△MDE是等腰三角形.
点评 此题是三角形综合题,主要考查了等腰三角形的性质,三角形的内角和定理,对称的性质,线段的垂直平分线的性质,全等三角形的判定和性质,解本题的关键是得出∠DCE=90°-$\frac{1}{2}$∠ACB,判定△CPE≌△CQD,是解本题的难点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
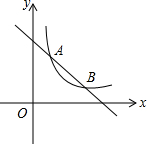 如图,在平面直角坐标系中,一次函数y=-x+m与反比例函数$y=\frac{k}{x}$的图象交于点A(1,3a),B(3,a).
如图,在平面直角坐标系中,一次函数y=-x+m与反比例函数$y=\frac{k}{x}$的图象交于点A(1,3a),B(3,a).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列运算正确的是( )
A. x3•x2=x6 B. (ab)2=ab2 C. a6+a6=a12 D. b2+b2=2b2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com