
【题目】在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,直线
轴的负半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() .
.
(1)如图1,求直线![]() 的解析式;
的解析式;

(2)如图2,连接![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 方向以1个单位/秒的速度向终点
方向以1个单位/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围.
的取值范围.

科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为﹣ ![]()
其中正确的结论个数有( )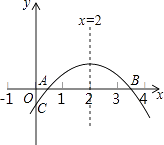
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(Ⅰ)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(Ⅱ)用描点法画函数图象:
(i)列表:
x | … | ﹣5 | ﹣2 | ﹣1 | 0 | … | 2 | 3 | 4 | 7 | … |
y | … | a | 2 | 3 | b | … | 6 | 3 | 2 | 1 | … |
表中a的值为 ,b的值为 .
(ii)描点连线:请在下图画出该图象的另一部分.

(Ⅲ)观察函数图象,得到函数![]() 的性质:
的性质:
当x 时,函数值y随x的增大而 ;
当x 时,函数值y随x的增大而减少.
(IV)应用:若![]() ≥6,则x的取值范围是 .
≥6,则x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,某市坚持绿色发展理念,着力建设生态典范城市,大力开展绿化工程建设.某校“社会实践”小组的同学为了了解该市绿地的发展情况,对市园林局进行了走访调查,获取了如下信息:
信息1:2015年的绿地总面积(绿地总面积=森林面积+草场面积)为276km2 , 其中森林面积比上一年增长40%,草地面积比上一年增长20%.
信息2:2014年的绿地总面积为200km2 . 
求:
(1)该市2014年的森林面积和草场面积分别为多少km2?
(2)若该市2016年的绿地总面积为338km2 , 求2014年至2016年该市绿地总面积的年平均增长率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从![]() 地出发向
地出发向![]() 地行走,同时晓阳从
地行走,同时晓阳从![]() 地出发向
地出发向![]() 地行走,如图所示,相交于点
地行走,如图所示,相交于点![]() 的两条线段
的两条线段![]() 、
、![]() 分别表示小明、晓阳离
分别表示小明、晓阳离![]() 地的距离
地的距离![]() (千米)与已用时间
(千米)与已用时间![]() (分钟)之间的关系.
(分钟)之间的关系.
(1)小明与晓阳相遇时,晓阳出发的时间是__________;
(2)求晓阳到达![]() 地的时间.
地的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市南县大力发展农村旅游事业,全力打造“洞庭之心湿地公园”,其中罗文村的“花海、涂鸦、美食”特色游享誉三湘,游人如织.去年村民罗南洲抓住机遇,返乡创业,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮利润是住宿利润的2倍还多1万元.
(1)求去年该农家乐餐饮和住宿的利润各为多少万元?
(2)今年罗南洲把去年的餐饮利润全部用于继续投资,增设了土特产的实体店销售和网上销售项目.他在接受记者采访时说:“我预计今年餐饮和住宿的利润比去年会有10%的增长,加上土特产销售的利润,到年底除收回所有投资外,还将获得不少于10万元的纯利润.”请问今年土特产销售至少有多少万元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共1000件,其进价和售价如下表所示:
甲 | 乙 | |
进价(元/件) | 15 | 35 |
售价(元/件) | 18 | 44 |
(1)若商店计划销售完这批商品后能获利4200元,则甲、乙两种商品应分别购进多少件;
(2)若该商店销售完这批商品后获利要多于5000元,则至少应购进乙种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与证明:

如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断线段MD与MN的关系,得出结论;
结论:DM、MN的关系是: ;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C旋转180°,其他条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com