
 如图,△ABC中,D在BC上,AB=AD,AE=AC,∠1=∠2.求证:∠EDC=∠1.
如图,△ABC中,D在BC上,AB=AD,AE=AC,∠1=∠2.求证:∠EDC=∠1. 分析 根据在△ABC中,D为BC上的一点,AB=AD,AE=AC,∠1=∠2,求证△AED≌△ACD,然后利用等量代换即可求的结论.
解答 证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
在△AED与△ACD中
$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAE}\\{AE=AC}\end{array}\right.$,
∴△AED≌△ACD(SAS),
∴∠B=∠ADE,
∵AB=AD,
∴∠B=∠ADB,
∴∠B+∠ADB+∠EDC=∠B+∠ADB+∠1=180°,
∴∠1=∠EDC
点评 此题考查全等三角形的判定和性质,关键是对全等三角形的判定与性质和等腰三角形的判定的理解和掌握.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:解答题
 已知:抛物线C1:y=x2-2x-3.
已知:抛物线C1:y=x2-2x-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
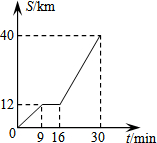 如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )
如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com