Question

1．如图1，菱形ABCD中，AB=5，AE⊥BC于E，AE=4．一个动点P从点B出发，以每秒1个单位长度的速度沿线段BC方向运动，过点P作PQ⊥BC，交折线段BA-AD于点Q，以PQ为边向右作正方形PQMN，点N在射线BC上，当P点到达C点时，运动结束．设点P的运动时间为t秒（t＞0）．
（1）求出线段BD的长，并求出当正方形PQMN的边PQ恰好经过点A时，运动时间t的值；
（2）在整个运动过程中，设正方形PQMN与△BCD的重合部分面积为S，请直接写出S与t之间的函数关系式和相应的自变量的取值范围；
（3）如图2，当点M与点D重合时，线段PQ与对角线BD交于点O，将△BPO绕点O逆时针旋转α°（0＜α＜180），记旋转中的△BPO为△B′P′O，在旋转过程中，设直线B′P′与直线BC交于G，与直线BD交于点H，是否存在这样的G、H两点，使△BGH为等腰三角形？若存在，求出此时OH²的值；若不存在，请说明理由．

Answer 1

分析 （1）过点D作DK⊥BC延长线于K．由夹在两条平行线间的平行线断相等可知DK=AE=4，依据勾股定理可求得CK的长，然后在△BKD中，依据勾股定理可求得BD的长；在Rt△ABE中，依据勾股定理可求得BE=3，从而可求得t的值；
（2）当点N在BC上时，如图2所示：过点F作FG⊥AB，垂足为G．先依据勾股定理求得BE的长，从而得到tan∠ABE的值，接下来，可利用含t的式子表示出PQ、PN的长，然后依据角平分线的性质可证明FG=FE，然后依据面积法可求得EF的长，于是可求得tan∠DBP的值，从而可用含t的式子表示出PH、IN的长，然后依据梯形的面积公式可求得S与t的函数关系；如图3所示：依据S=S_{四边形HPNI}-S_△CNG求解即可；如图4所示：依据S=S_{四边形HPNI}-S_△CNG求解即可；如图5所示：过点C作CF⊥BC，交DB与点F，交AD于点G．依据S=S_{四边形HPCF}+S_△DFC求解即可；
（3）当点M与点D重合时，先求得PO和BO的长，如图6所示：当HB=HG时．先证明HO=HB'．然后在Rt△OHP′中，由勾股定理可知：可求得OH的长，从而可求得答案；如图7所示：当GB=GH时．点G与点C重合，点H与点D重合，故此可得到OH=2$\sqrt{5}$；如图8所示：当BH=BG时．先证明OB′=HB′=OB，由旋转的性质可知求得P′B′、OP′的长，从而可求得HP′的长，最后在△OHP′中，依据勾股定理可求得OH的长；如图9所示：当BH=BG时．

解答 解：（1）如图1所示：过点D作DK⊥BC延长线于K．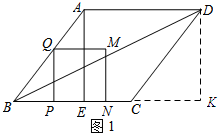

∵AE∥DK，AD∥EC，
∴DK=AE=4．
∵Rt△DKC中，CD=5，DK=4，
∴CK=3，
∴BK=5+3=8，
∴Rt△DBK中，BD=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{5}$．
∵在Rt△ABE中，AB=5，AE=4，
∴BE=3，
∴当点Q与点A重合时，t=3．
（2）①当点N在BC上时，如图2所示：过点F作FG⊥AB，垂足为G．

∵在Rt△ABE中，AB=5，AE=4，
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=3．
∵AE∥PQ，
∴$\frac{PQ}{BP}=\frac{AE}{BE}$，
∴$\frac{PQ}{t}=\frac{4}{3}$，
∴PQ=PN=$\frac{4}{3}$t，BN=$\frac{7}{3}$t．
∵四边形ABCD为菱形，
∴BD是∠ABC的平分线．
又∵FE⊥BC，FG⊥AB，
∴FG=FE．
∴$\frac{1}{2}$BE•EF+$\frac{1}{2}$AB•FG=$\frac{1}{2}$BE•EF+$\frac{1}{2}$AB•EF=$\frac{1}{2}$BE•AE．
∴3EF+5EF=12，解得EF=$\frac{3}{2}$．
∴tan∠DBC=$\frac{1}{2}$．
∴PH=$\frac{1}{2}$t，NI=$\frac{7}{6}$t．
∴S=$\frac{1}{2}$（PH+IN）•PN=$\frac{1}{2}$（$\frac{1}{2}$t+$\frac{7}{6}$t）•$\frac{4}{3}$t=$\frac{10}{9}$t²．
∵当点N在BC上，
∴PN≤5，即$\frac{7}{3}$t≤5，解得t≤$\frac{15}{7}$．
∴当0＜t≤$\frac{15}{7}$时，S=$\frac{10}{9}$t²．
当$\frac{15}{7}$＜t≤3时，如图3所示：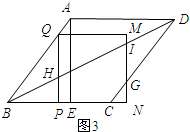

∵BN=$\frac{7}{3}$t，BC=5，
∴CN=$\frac{7}{3}$t-5．
∴GN=$\frac{4}{3}$CN．
∴S=S_{四边形HPNI}-S_△CNG=$\frac{10}{9}$t²-$\frac{1}{2}$×$\frac{4}{3}$×（$\frac{7}{3}$t-5）²=-$\frac{68}{27}$t²+$\frac{140}{9}$t-$\frac{50}{3}$（$\frac{15}{7}$＜t≤3）．
如图4所示：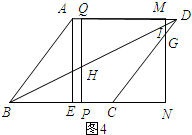

∵PB=t，PN=4，
∴BN=t+4，CN=t+4-5=t-1．
∴PH=$\frac{1}{2}$t，IN=$\frac{1}{2}$t+2．
∴S=S_{四边形HPNI}-S_△CNG=$\frac{1}{2}$×4×（$\frac{1}{2}$t+$\frac{1}{2}$t+2）-$\frac{1}{2}$×$\frac{4}{3}$（t-1）²=-$\frac{2}{3}$t²+$\frac{10}{3}$t+$\frac{10}{3}$（3＜t≤4）．
如图5所示：过点C作CF⊥BC，交DB与点F，交AD于点G．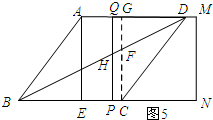

∵BC=5，BP=t，
∴PH=$\frac{1}{2}$t，FC=$\frac{5}{2}$，PC=5-t．
∵AG=EC=2，
∴DG=3．
∴S=S_{四边形HPCF}+S_△DFC=$\frac{1}{2}$×（$\frac{1}{2}$t+$\frac{5}{2}$）（5-t）+$\frac{1}{2}$×$\frac{5}{2}$×3=-$\frac{1}{4}$t2+10（4＜t≤5）．
综上所述，S与t之间的函数关系式为$S=\left\{\begin{array}{l}\frac{10}{9}{t^2}（0＜t≤\frac{15}{7}）\\-\frac{68}{27}{t^2}+\frac{140}{9}t-\frac{50}{3}（\frac{15}{7}＜t≤3）\\-\frac{2}{3}{t^2}+\frac{10}{3}t+\frac{10}{3}（3＜t≤4）\\-\frac{1}{4}{t^2}+10（4＜t≤5）\end{array}\right.$．
（3）当点M与点D重合时．
BP=QM=4，∠BPO=∠MQO，∠BOP=∠MOQ
∴△BPO≌△MQO
∴PO=2，BO=$2\sqrt{5}$
如图6所示：当HB=HG时．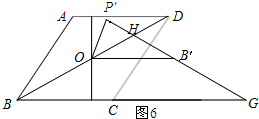

∵HB=HG，
∴∠HBC=∠HGB．
∵由旋转的性质可知：∠HBC=∠OB′P′，
∴∠OB′P′=∠HGB．
∴OB'∥BG．
∴∠HOB′=∠HB′O．
∴HO=HB'．
设HO=HB'=x，则
在Rt△OHP′中，由勾股定理可知：OH²=OP′²+HP′²，即x²=2²+（4-x）²，
解得：$x=\frac{5}{2}$
∴$O{H^2}=\frac{25}{4}$．
如图7所示：当GB=GH时．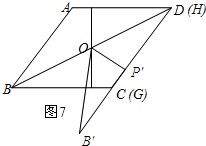

∵GB=GH，
∴∠GBH=∠GHB
∴此时，点G与点C重合，点H与点D重合
∴OH²=OD²=（2$\sqrt{5}$）²=20．
如图8所示：当BH=BG时．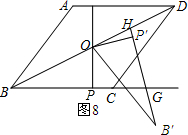

∵BH=BG，
∴∠BGH=∠BHG．
∵∠HBG=∠B'，
∴∠HOB'=∠OHB'
∴HB'=OB'=$2\sqrt{5}$，
∴HP'=$2\sqrt{5}-4$．
∴$O{H^2}={2^2}+{（2\sqrt{5}-4）^2}=40-16\sqrt{5}$．
如图9所示：当BH=BG时．

∵BH=BG，
∴∠BGH=∠H
∴∠OBG=∠OB'P'=2∠H
∴∠HOB'=∠H
∴HB'=OB'=$2\sqrt{5}$，
∴HP'=$2\sqrt{5}+4$．
∴$O{H^2}={2^2}+{（2\sqrt{5}+4）^2}=40+16\sqrt{5}$．
综上所述，当$O{H^2}=\frac{25}{4}$、20、$40-16\sqrt{5}$、$40+16\sqrt{5}$时，△BGH为等腰三角形．

点评 本题是一道几何变形的综合题，解答本题主要应用了勾股定理、旋转的性质、翻折的性质、等腰三角形的性质和判断，根据题意画出符合题意的图形是解题的关键．