
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树状图或列表法中的一种列举出这两中的一种列举出这辆汽车行驶方向所有可能的结果;
(2)求至少有一辆汽车向左转的概率.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,以![]() 为斜边作
为斜边作![]() 和
和![]() ,
,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,点
,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() 分别交
分别交![]() 于
于![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长;
的长;
(3)若![]()
![]() ,
,![]()
![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班甲、乙两名同学在5次引体向上测试中的有效次数如下:
甲:8,8,7,8,9.乙:5,9,7,10,9.
甲、乙两同学引体向上的平均数、众数、中位数、方差如下:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 |
| 8 | 0.4 |
乙 |
| 9 |
| 3.2 |
根据以上信息,回答下列问题:
(1)表格中![]() _______,
_______,![]() _______,
_______,![]() _______.(填数值)
_______.(填数值)
(2)体育老师根据这5次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是_______________________________________.班主任李老师根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是_______________________________________.
(3)乙同学再做一次引体向上,次数为n,若乙同学6次引体向上成绩的中位数不变,请写出n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.

(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D, 连接BE,过点O作OC∥BE交切线DE于点C,连接AC .

(1)求证:AC是⊙O的切线 ;
(2)若BD=OB=4,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行于⊙O的弦MB,连接DM并延长交x轴于点C.
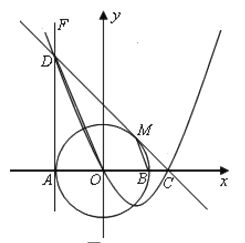
(1)判断直线DC与⊙O的位置关系,并给出证明;
(2)设点D的坐标为(-2,4),试求经过D、O、C三点的抛物线的解析式.
(3)若坐标平面内的点P,使得以点P和三点D、O、C为顶点的四边形是平行四边形,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
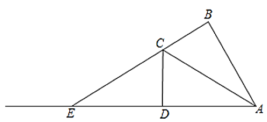
【题目】如图,在四边形ABCD中,AC是对角线,∠ABC=∠CDA=90°,BC=CD,延长BC交AD的延长线于点E.
(1)求证:AB=AD;
(2)若AE=BE+DE,求∠BAC的值;
(3)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P,连接PB.设PB=a,点O是直线AE上的动点,当MO+PO的值最小时,点O与点E是否可能重合?若可能,请说明理由并求此时MO+PO的值(用含a的式子表示);若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.

根据以上信息解决下列问题:
(1)![]() ,
,![]() ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的![]() 名学生中恰好有
名学生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形ABCD折叠,使点A与CD边上的点H重合(H不与C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD周长为m,△CHG周长为n,则![]() 的值为( )
的值为( )
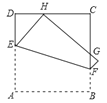
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com