
【题目】如图,已知在四边形ABCD中,AD=BC且AC⊥BD,点E,F,G,H,P,Q分别是AB,BC,CD,DA,AC,BD的中点.
求证:(1)四边形EFGH是矩形;
(2)四边形EQGP是菱形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)已知点E,F,G,H分别为AB,BC,CD,DA的中点,根据三角形的中位线定理可得EF∥AC,GF∥BD,GH∥AC,EH∥BD,所以EF∥GH,GF∥EH,根据两组对边分别平行的四边形是平行四边形,即可判定四边形EFGH是平行四边形;(2)已知点E,P,G,Q分别为AB,AC,DC,DB的中点,根据三角形的中位线定理可得EP=![]() BC,PG=
BC,PG=![]() AD,GQ=
AD,GQ=![]() BC,QE=
BC,QE=![]() AD,又因AD=BC,所以EP=PG=GQ=QE,即可判定四边形EQGP是菱形.
AD,又因AD=BC,所以EP=PG=GQ=QE,即可判定四边形EQGP是菱形.
试题解析:
(1)∵点E,F,G,H分别为AB,BC,CD,DA的中点,
∴EF∥AC,GF∥BD,GH∥AC,EH∥BD,
∴EF∥GH,GF∥EH,∴四边形EFGH是平行四边形.
又∵AC⊥BD,∴EF⊥EH.∴EFGH是矩形.
(2)∵点E,P,G,Q分别为AB,AC,DC,DB的中点,
∴EP=![]() BC,PG=
BC,PG=![]() AD,GQ=
AD,GQ=![]() BC,QE=
BC,QE=![]() AD.
AD.
∵AD=BC,∴EP=PG=GQ=QE,∴四边形EQGP是菱形.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,投掷这样的骰子一次,向上一面点数是偶数的结果有( )
A.1种
B.2种
C.3种
D.6种
查看答案和解析>>
科目:初中数学 来源: 题型:
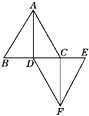
【题目】如图,已知△ABC和△DEF是两个边长都为1 cm的等边三角形,且B,D,C,E都在同一直线上,连接AD及CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=0.3 cm,△ABC沿着BE的方向以每秒1 cm的速度运动,设△ABC的运动时间为t秒.
①当t为何值时, ![]() ADFC是菱形?请说明你的理由;
ADFC是菱形?请说明你的理由;
②![]() ADFC有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
ADFC有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列式计算:已知三角形的第一条边长为5a+3b,第二条边比第一条边短2a-b,第三条边比第二条边短a-b.
(1)求第二条边长;
(2)求这个三角形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com