
| A. | 3 | B. | -3 | C. | 5 | D. | -5 |
分析 根据方程的解析式结合根与系数的关系找出a+b=3、ab=p,利用完全平方公式将a2-ab+b2=18变形成(a+b)2-3ab=18,代入数据即可得出关于p的一元一次方程,解方程即可得出p的值,经验证p=-3符合题意,再将$\frac{a}{b}$+$\frac{b}{a}$变形成$\frac{(a+b)^{2}}{ab}$-2,代入数据即可得出结论.
解答 解:∵a、b为方程x2-3x+p=0(p≠0)的两个不相等的实数根,
∴a+b=3,ab=p,
∵a2-ab+b2=(a+b)2-3ab=32-3p=18,
∴p=-3.
当p=-3时,△=(-3)2-4p=9+12=21>0,
∴p=-3符合题意.
$\frac{a}{b}$+$\frac{b}{a}$=$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$=$\frac{(a+b)^{2}}{ab}$-2=$\frac{{3}^{2}}{-3}$-2=-5.
故选D.
点评 本题考查了根与系数的关系、解一元一次方程以及完全平方公式的应用,解题的关键是求出p=-3.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系找出两根之和与两根之积是关键.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 3+$\sqrt{3}$=3$\sqrt{3}$ | B. | $\sqrt{{{(-2)}^2}}$=2 | C. | $\sqrt{50}$=$\sqrt{25+25}$=5+5=10 | D. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
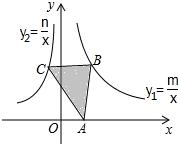 如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )
如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )| A. | 当点A保持不动,点C,B随意移动时,△ABC的面积不变 | |
| B. | 当点A移动,BC保持不动时,△ABC的面积不变 | |
| C. | 不管点A,B,C怎么移动,△ABC的面积始终不变 | |
| D. | 不管点A,B,C怎么移动,只要BC与x轴平行,△ABC的面积就不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
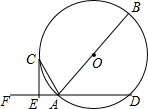 如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
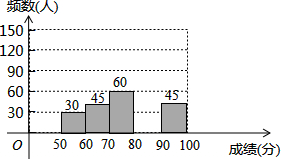 为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:| 组别 | 分数段 | 频数(人) | 频率 |
| 1 | 50≤x<60 | 30 | 0.1 |
| 2 | 60≤x<70 | 45 | 0.15 |
| 3 | 70≤x<80 | 60 | n |
| 4 | 80≤x<90 | m | 0.4 |
| 5 | 90≤x<100 | 45 | 0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com