
【题目】如图,点![]() 是线段
是线段![]() 上的任意一点(
上的任意一点(![]() 点不与
点不与![]() 点重合),分别以
点重合),分别以![]() 为边在直线
为边在直线![]() 的同侧作等边三角形
的同侧作等边三角形![]() 和等边三角形
和等边三角形![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
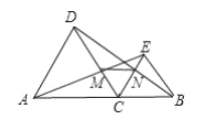
(1)求证: ![]() ;
;
(2)求证: ![]() ;
;
(3)若![]() 的长为12cm,当点
的长为12cm,当点![]() 在线段
在线段![]() 上移动时,是否存在这样的一点
上移动时,是否存在这样的一点![]() ,使线段
,使线段![]() 的长度最长?若存在,请确定
的长度最长?若存在,请确定![]() 点的位置并求出
点的位置并求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)见解析;(2) 见解析;(3) 存在,请确定C点的位置见解析,MN=3.
【解析】
(1)根据题意证明△DCB≌△ACE即可得出结论;
(2)由题中条件可得△ACE≌△DCB,进而得出△ACM≌△DCN,即CM=CN,△MCN是等边三角形,即可得出结论;
(3)可先假设其存在,设AC=x,MN=y,进而由平行线分线段成比例即可得出结论.
解:(1)∵△ACD与△BCE是等边三角形,
∴AC=CD,CE=BC,
∴∠ACE=∠BCD,
在△ACE与△DCB中,
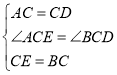 ,
,
∴△ACE≌△DCB(SAS),
∴DB=AE;
(2)∵△ACE≌△DCB,
∴∠CAE=∠BDC,
在△ACM与△DCN中,
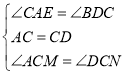 ,
,
∴△ACM≌△DCN,
∴CM=CN,
又∵∠MCN=180°-60°-60°=60°,
∴△MCN是等边三角形,
∴∠MNC=∠NCB=60°
即MN∥AB;
(3)解:假设符合条件的点C存在,设AC=x,MN=y,
∵MN∥AB,
∴![]() ,
,
即![]() ,
,
![]() ,
,
当x=6时,ymax=3cm,
即点C在点A右侧6cm处,且MN=3.


科目:初中数学 来源: 题型:
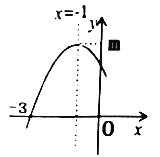
【题目】二次函数![]() 图象的一部分如图所示,顶点坐标为
图象的一部分如图所示,顶点坐标为![]() ,与
,与![]() 轴的一个交点的坐标为(-3,0),给出以下结论:①
轴的一个交点的坐标为(-3,0),给出以下结论:①![]() ;②
;②![]() ;③若
;③若![]() 、
、![]() 为函数图象上的两点,则
为函数图象上的两点,则![]() ;④当
;④当![]() 时方程
时方程![]() 有实数根,则
有实数根,则![]() 的取值范围是
的取值范围是![]() .其中正确的结论的个数为( )
.其中正确的结论的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为F,CG⊥AE,交弦AE的延长线于点G,且CG=CF.
(1)求证:CG是⊙O的切线;
(2)若AE=2,EG=1,求由弦BC和![]() 所围成的弓形的面积.
所围成的弓形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
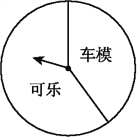
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
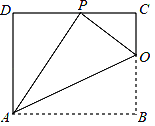
【题目】如图,已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的点P处,折痕与BC交于点O.
(1)求证:△OCP∽△PDA;
(2)若PO:PA=1:2,则边AB的长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产化肥的总任务一定,平均每天化肥产量y(吨)与完成生产任务所需要的时间x(天)之间成反比例关系,如果每天生产化肥125吨,那么完成总任务需要7天.
(1)求y关于x的函数表达式,并指出比例系数;
(2)若要5天完成总任务,则每天产量应达到多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() (k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①对角线互相垂直的四边形是菱形;②若![]() ,则
,则![]() ;③两个位似图形一定是相似图形;④若
;③两个位似图形一定是相似图形;④若![]() ,则
,则![]() ;其中原命题是真命题逆命题是假命题的有( )
;其中原命题是真命题逆命题是假命题的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com