
 如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.
如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.分析 (1)由已知各件,据AAS很容易证得:△BDE≌△CDF;
(2)连接BF、CE,由AB=AC,D是BC边的中点,可知AD⊥BC,易证得△BFD≌△CFD,可得BF=CF;又因为(1)中△BDE≌△CDF得ED=FD,所以EF、BC互相垂直平分,根据菱形的性质,可得四边形BECF是菱形.
解答 (1)证明:∵在△ABC中,D是BC边的中点,
∴BD=CD,
∵CF∥BE,
∴∠CFD=∠BED,
在△CFD和△BED中,
$\left\{\begin{array}{l}{∠CFD=∠BED}&{\;}\\{CD=BD}&{\;}\\{∠FDC=∠EDB}&{\;}\end{array}\right.$,
∴△CFD≌△BED(AAS),
∴CF=BE,
∴四边形BFCE是平行四边形;
(2)解:当AB=AC时,四边形BECF是菱形;理由如下:
∵AB=AC,D是BC边的中点,
∴AD⊥BC,
∴EF⊥BC,
∴四边形BECF是菱形.
点评 本题主要考查了菱形的判定、平行四边形的判定、全等三角形的判定与性质、平行线的性质、等腰三角形的性质;熟练掌握菱形的判定方法或等腰三角形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:选择题
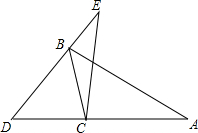 如图,在△ABC中,∠A=30°,∠ABC=50°,∠ACB=100°,△EDC≌△ABC,且A、C、D在同一条直线上,则∠BCE=( )
如图,在△ABC中,∠A=30°,∠ABC=50°,∠ACB=100°,△EDC≌△ABC,且A、C、D在同一条直线上,则∠BCE=( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,若AB=6,AC=5,则△ADE的周长为( )
如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,若AB=6,AC=5,则△ADE的周长为( )| A. | 8 | B. | 8.5 | C. | 9 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
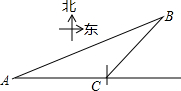 钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10$\sqrt{2}$海里,求AC的距离.(结果保留根号)
钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10$\sqrt{2}$海里,求AC的距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5cm | B. | 4cm | C. | 3cm | D. | 4.8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?
如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com