
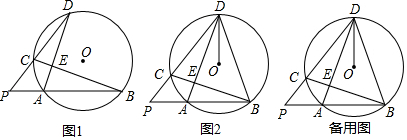
分析 (1)根据已知条件得到∠D+∠B+∠P=90°,根据外角的性质得到∠D+∠DCE=90°,由垂直的定义即可得到结论;
(2)如图2,延长DO交⊙O于G,根据角平分线的定义得到∠CDA=∠ADG,根据余角的性质得到∠DAB=∠G,等量代换得到∠DAB=∠ABD,根据等腰三角形的判定即可得到结论;
(3)如图,过点O作OM⊥AD于点M,交CD于点H,连接AH.根据角平分线的性质得到DH=OD=5,由垂径定理可知OH垂直平分AD,于是得到AH=DH=OD=5,AM=DM,推出∠PAH=90°,得到PA=$\frac{15}{4}$,由(2)可知:∠PHA=∠BDE,根据三角函数的定义设BE=3m,DE=4m,AD=BD=5m,求得AM=DM=$\frac{5m}{2}$,根据勾股定理得到m2=$\frac{18}{5}$,于是得到结论.
解答 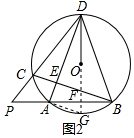 解:(1)∵2∠PDA+∠P=90°,∠D=∠B,
解:(1)∵2∠PDA+∠P=90°,∠D=∠B,
∴∠D+∠B+∠P=90°,
∵∠DCE=∠P+∠B,
∴∠D+∠DCE=90°,
∴∠CED=90°,
∴AD⊥BC;
(2)如图2,延长DO交⊙O于G,
∴∠DAG=90°,
∴∠G+∠ADG=90°,
∵AD平分∠ODC,
∴∠CDA=∠ADG,
∵∠ADG=∠ABC,
∵∠DAB+∠ABC=90°,
∴∠DAB=∠G,
∵∠G=∠ABD,
∴∠DAB=∠ABD,
∴AD=BD;
(3)如图,过点O作OM⊥AD于点M,交CD于点H,连接AH.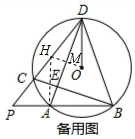
∵AD平分∠ODC,∴DH=OD=5,
∴由垂径定理可知:OH垂直平分AD,
∴AH=DH=OD=5,AM=DM,
∴∠HDA=∠HAD,
∴∠PHA=2∠HDA,
即:∠PHA=2∠PDA,
∵2∠PDA+∠P=90°,
∴∠PHA+∠P=90°,
∴∠PAH=90°,
∵PA=$\frac{15}{4}$,由(2)可知:∠PHA=∠BDE,
∴tan∠PHA=tan∠BDE=PA:AH=BE:DE=$\frac{15}{4}$:5=3:4,
设BE=3m,则:DE=4m,AD=BD=5m,
∴AM=DM=$\frac{5m}{2}$,
∴AE=AD-DE=m,
∵∠ABE=∠CDE=∠ODM,
∴tan∠ABC=tan∠CDE=tan∠ODM=AE:BE=CE:DE=OM:DM=m:3m=1:3,
∴CE=$\frac{4m}{3}$,OM=$\frac{5m}{6}$,∴BC=BE+CE=$\frac{13m}{3}$,
∵OM2+DM2=OD2,即($\frac{5m}{6}$)2+($\frac{5m}{2}$)2=52,
∴m2=$\frac{18}{5}$,
∴四边形ABDC的面积=$\frac{1}{2}$AD•BC=$\frac{1}{2}$×5m×$\frac{13m}{3}$=$\frac{65{m}^{2}}{6}$=39.
点评 本题考查了圆周角定理三角函数的定义,三角形的外角的性质,勾股定理,图形的面积的计算,正确的作出辅助线是解题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
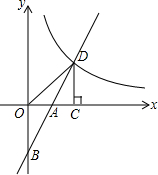 如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=$\frac{k}{x}$(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD.已知△AOB≌△ACD.
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=$\frac{k}{x}$(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD.已知△AOB≌△ACD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个数的绝对值相等,这两个数也相等 | |
| B. | 一个有理数若不是正数必定是负数 | |
| C. | 两个数不相等,这两个数的绝对值也不相等 | |
| D. | 互为相反数的两个数绝对值相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
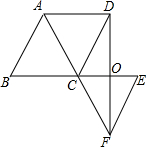 如图,延长?ABCD的边BC至点E,使CE=BC,连接AC并延长至点F,使CF=AC,连接EF、DF,DF交CE于O,求证:OD=OF.
如图,延长?ABCD的边BC至点E,使CE=BC,连接AC并延长至点F,使CF=AC,连接EF、DF,DF交CE于O,求证:OD=OF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
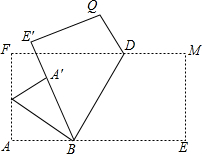 将一张长方形纸片的一角折叠,使点A落在A′处,BC为折痕,然后把BE折过去,使之与A′B重合,折痕为BD,那么两条折痕BC与BD的夹角是多少度?
将一张长方形纸片的一角折叠,使点A落在A′处,BC为折痕,然后把BE折过去,使之与A′B重合,折痕为BD,那么两条折痕BC与BD的夹角是多少度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com