
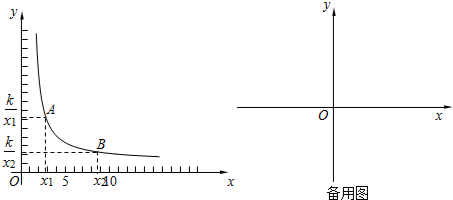
分析 (1)在反比例函数y=$\frac{k}{x}$(k>0)的图象上任取一点P(m,n),只需证明点P关于原点的对称点也在反比例函数y=$\frac{k}{x}$(k>0)的图象上即可;
(2)①在二次函数y=ax2(a>0,a为常数)的图象上任取一点Q(m,n),只需证明点Q关于y轴的对称点也在二次函数y=ax2(a>0,a为常数)的图象上,就可得到二次函数y=ax2(a>0,a为常数)关于y轴对称;②在二次函数y=ax2 (a>0,a为常数)的图象上任取两点A、B,设A(m,am2),B(n,an2),且0<m<n.只需运用分类讨论和作差法就可解决问题;
(3)只需运用作差法分别讨论0<x<1或x>1时函数的增减性,就可解决问题.
解答 解:(1)在反比例函数y=$\frac{k}{x}$(k>0)的图象上任取一点P(m,n),
则mn=k.点P关于原点的对称点为P1(-m,-n).
∵(-m)(-n)=mn=k,
∴点P1也必在这个反比例函数y=$\frac{k}{x}$的图象上.
∴反比例函数y=$\frac{k}{x}$(k>0)的图象关于原点对称;
(2)答案分别为:
(对称性)二次函数y=ax2(a>0,a为常数)的图象关于y轴成轴对称;
(增减性)当x>0时,y随x增大而增大;当x<0时,y随x增大而减小.
(说理)①∵在二次函数y=ax2(a>0,a为常数)的图象上任取一点Q(m,n),于是n=am2.
∴点Q关于y轴的对称点Q1(-m,n).
而n=a(-m)2,即n=am2.
这说明点Q1也必在在二次函数y=ax2(a>0,a为常数)的图象上.
∴二次函数y=ax2(a>0,a为常数)的图象关于y轴成轴对称;
②在二次函数y=ax2(a>0,a为常数)的图象上任取两点A、B,
设A(m,am2),B(n,an2),且0<m<n.
则an2-am2=a(n+m)(n-m),
∵n>m>0,
∴n+m>0,n-m>0;
∵a>0,
∴an2-am2=a(n+m)(n-m)>0,即an2>am2.
而当m<n<0时,n+m<0,n-m>0;
∵a>0,
∴an2-am2=a(n+m)(n-m)<0.即an2<am2.
这说明,当x>0时,y随x增大而增大;当x<0时,y随x增大而减小;
(3)在函数图象上任意取两点A、B,设A(x1,x12+$\frac{2}{{x}_{1}}$),B(x2,x22+$\frac{2}{{x}_{2}}$),
且0<x1<x2.
①当0<x1<x2<1时,
则有$\frac{2}{{x}_{1}•{x}_{2}}$>2,x1+x2<2,x1-x2<0,
∴x1+x2-$\frac{2}{{x}_{1}•{x}_{2}}$<0,
∴(x12+$\frac{2}{{x}_{1}}$)-(x22+$\frac{2}{{x}_{2}}$)=x12+$\frac{2}{{x}_{1}}$-x22-$\frac{2}{{x}_{2}}$=x12-x22+$\frac{2}{{x}_{1}}$-$\frac{2}{{x}_{2}}$=(x1+x2)(x1-x2)+$\frac{2{x}_{2}-2{x}_{1}}{{x}_{1}•{x}_{2}}$
=(x1-x2)(x1+x2-$\frac{2}{{x}_{1}•{x}_{2}}$)>0,
∴当0<x<1时,y随x的增大而减小;
②当1<x1<x2时,
则有$\frac{2}{{x}_{1}•{x}_{2}}$<2,x1+x2>2,x1-x2<0,
∴x1+x2-$\frac{2}{{x}_{1}•{x}_{2}}$>0,
∴(x12+$\frac{2}{{x}_{1}}$)-(x22+$\frac{2}{{x}_{2}}$)=x12+$\frac{2}{{x}_{1}}$-x22-$\frac{2}{{x}_{2}}$=x12-x22+$\frac{2}{{x}_{1}}$-$\frac{2}{{x}_{2}}$=(x1+x2)(x1-x2)+$\frac{2{x}_{2}-2{x}_{1}}{{x}_{1}•{x}_{2}}$
=(x1-x2)(x1+x2-$\frac{2}{{x}_{1}•{x}_{2}}$)<0,
∴当x>1时,y随x的增大而增大;
∴当x=1时函数取得最小值.
点评 本题主要考查了函数的对称性、增减性、因式分解等知识,运用分类讨论和作差法是解决本题的关键.


科目:初中数学 来源: 题型:解答题
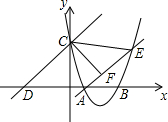 如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.
如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
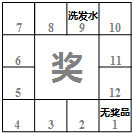 大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.
大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
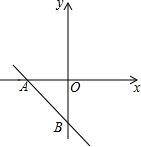 如图,在平面直角坐标系中,一次函数y=-x-3分别与x轴、y轴相交于A、B两点,二次函数y=x2+mx+n(m≠6)的图象经过点A.
如图,在平面直角坐标系中,一次函数y=-x-3分别与x轴、y轴相交于A、B两点,二次函数y=x2+mx+n(m≠6)的图象经过点A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>1 | B. | x<$\frac{1}{4}$ | C. | $\frac{1}{4}$<x<1 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com