
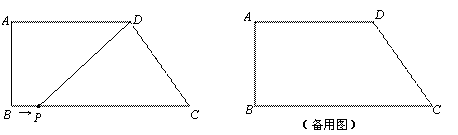
如图,直角梯形ABCD,AD∥BC,∠B=90º,AD=6,AB=4,
BC=9.
(1)CD的长为 .
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?
(3)在(2)的条件下,点Q同时从点B出发,以每秒4个单位的速度沿着边BA、AD向点D运动,当点Q到达终点时两点同时停止运动.是否存在某一时刻t,使得以点P、Q、D、C为顶点的四边形是平行四边形?若存在,请求出t的值;若不存在,请说明理由.
 |
(2)过点D作DE⊥BC,垂足为E,由题意得PC=9—t,PE=6—t.
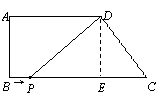 当CD=CP时,5=9—t,解得t=4;
当CD=CP时,5=9—t,解得t=4;
当CD=PD时,E为PC中点,
∴6—t=3,∴t=3;
当PD=PC时,PD2=PC2,
∴(6—t)2+42=(9—t)2,解得t=![]() .
.
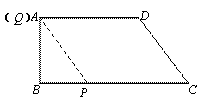 (3)显然,当点Q在AB上时,以点P、Q、D、C为顶点的四边形不可能是平行四边形;
(3)显然,当点Q在AB上时,以点P、Q、D、C为顶点的四边形不可能是平行四边形;
当点Q在AD上时,1≤t<![]() .
.
若四边形PQDC为平行四边形,则PC=DQ.
∴9—t=10—4t,解得t=![]() (不合题意,舍去).
(不合题意,舍去).
∴不存在某一时刻t,使得以点P、Q、D、C为顶点的四边形是平行四边形.(7分)
当3≤v<![]() 时,在整个运动过程中,始终存在某一时刻,使四边形PQDC为平行四边形.
时,在整个运动过程中,始终存在某一时刻,使四边形PQDC为平行四边形.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.查看答案和解析>>
科目:初中数学 来源: 题型:
 ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com