
分析 (1)根据15(8)=1×81+5×80=13,即可得出八进制的15转化成十进制的数为13;根据98÷92=1…17,17÷91=1…8,即可得出十进制的98转化成九进制的数为118;
(2)①算出当x=7时,十进制两位数的值,再将其转换成八进制的两位数,即可得出y值;
②将九进制的两位数与八进制的两位数均转换成十进制两位数,令其相等即可得出x、y之间的关系,根据x≤8即可得出x的值,套入数据即可得出结论.
解答 解:(1)∵15(8)=1×81+5×80=13,
∴15(8)=13(10);
∵98÷92=1…17,17÷91=1…8,
∴98(10)=118(9).
故答案为:13;118.
(2)①2x(9)=2×9+x=25,
25÷81=3…1,
∴y=1.
故答案为:1.
②由题意得:九进制两位数和八进制两位数分别是2x和3y,
则2×9+x=3×8+y,
∴x=6+y,
∵x≤8,
∴x=6、7、8.
则九进制数分别是26、27、28.
∴十进制两位数分别是24、25、26.
点评 本题考查了二元一次方程的应用,解题的关键是:(1)弄明白各进制之间的转换;(2)①求出十进制两位数的值;②找出x、y之间的关系式.本题属于中档题,难度不大,解决该题型题目时,能够熟练将各进制之间的数进行转换是关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
| 每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
| 人数 | 1 | 1 | 2 | 6 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知在△ABC中,AB=1,BC=4$\sqrt{\frac{1}{2}}$,CA=$\frac{1}{5}$$\sqrt{125}$.
已知在△ABC中,AB=1,BC=4$\sqrt{\frac{1}{2}}$,CA=$\frac{1}{5}$$\sqrt{125}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等.(不写作法,但要保留作图痕迹)
青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等.(不写作法,但要保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
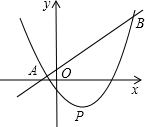 如图,直线y=kx+2k-1与抛物线y=kx2-2kx-4(k>0)相交于A,B两点,抛物线的顶点为P.
如图,直线y=kx+2k-1与抛物线y=kx2-2kx-4(k>0)相交于A,B两点,抛物线的顶点为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,六盘水高铁站在南宁市45°扇形辐射区域内,要求到“昆明”和“贵阳”的距离相等,又同时保证高铁站到“云广连线”和“贵广连线”距离相同.
如图所示,六盘水高铁站在南宁市45°扇形辐射区域内,要求到“昆明”和“贵阳”的距离相等,又同时保证高铁站到“云广连线”和“贵广连线”距离相同.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com