
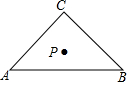
 如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )
如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
科目:初中数学 来源: 题型:选择题

| A. | (2017,0) | B. | (2017$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | C. | (2018,$\sqrt{3}$) | D. | (2018,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
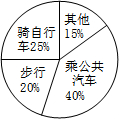 某校学生到校方式情况的统计图如图所示,若该校步行到校的学生有100人,则乘公共汽车到校的学生有( )
某校学生到校方式情况的统计图如图所示,若该校步行到校的学生有100人,则乘公共汽车到校的学生有( )| A. | 75人 | B. | 100人 | C. | 125人 | D. | 200人 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
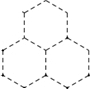 如图,是由大小完全相同的正六边形组成的图形,小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色,则上方的正六边形涂红色的概率是$\frac{1}{3}$.
如图,是由大小完全相同的正六边形组成的图形,小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色,则上方的正六边形涂红色的概率是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
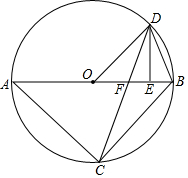 如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com