
����Ŀ����ͼ1���������ϵ�A����B��Ӧ�����ֱ���6����6����DCE��90������C���O�غϣ���D��������������ϣ�
��1����ͼ1����CFƽ�֡�ACE�����AOF���� ���ȣ���A���B�ľ���=��
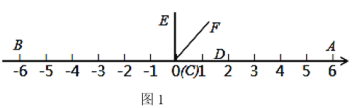
��2����ͼ2������DCE�����������������ƽ��t��0��t��3������λ�����Ƶ㶥��C��ʱ����ת30t�ȣ���CFƽ�֡�ACE����ʱ�ǡ�DCF������

����t��1ʱ�������� ������B���C�ľ���=��
��������BCE������������ϵ����˵�����ɣ�
��3����ͼ3����ʼ��D1C1E1���DCE�غϣ�����DCE�����������������ƽ��t��0![]() t
t![]() 3������λ�����Ƶ㶥��C��ʱ����ת30t�ȣ���CFƽ�֡�ACE����ʱ�ǡ�DCF���������ͬʱ������D1C1E1������ĸ���������ƽ��t��0
3������λ�����Ƶ㶥��C��ʱ����ת30t�ȣ���CFƽ�֡�ACE����ʱ�ǡ�DCF���������ͬʱ������D1C1E1������ĸ���������ƽ��t��0![]() t
t![]() 3������λ�����Ƶ㶥��C1˳ʱ����ת30t�ȣ���C1F1ƽ�֡�AC1E1���ǡ�D1C1F1������������������|������|��20������t��ֵ��
3������λ�����Ƶ㶥��C1˳ʱ����ת30t�ȣ���C1F1ƽ�֡�AC1E1���ǡ�D1C1F1������������������|������|��20������t��ֵ��

���𰸡���1��45����12����2����30����8����![]() �����ɼ���������3��
�����ɼ���������3��![]()
��������
��1�����ݽ�ƽ���ߵĶ�������AOF������������������룻
��2���ٸ��ݡ�FCD����ACF��ACD�������ACF����ACD���ɣ������������ɼ�����룻
�ڲ��룺��BCE��2�������ݡ�BCE����AOB��ECD��ACD���㼴�ɣ�
��3���������������t��ʾ�����������̼��ɽ�����⣻
��1���ߡ�DCE��90����CFƽ�֡�ACE��
���AOF��45����
���Ϊ��45�㣻
��A���B�ľ���Ϊ12��
�����12��
��2���ٵ�t��1ʱ��
��FCD����ACF��ACD=75��-45��=30�㣬
���Ϊ��30�㣻
��B���C�ľ���8��
�����8��
�ڲ��룺��BCE��![]() ��
��
�������£��ߡ�DCE��90������DCF��![]() ��
��
���ECF��90��-![]() ��
��
��CFƽ�֡�ACE��
���ACF����ECF��90��-![]() ��
��
�ߵ�A��O��B����
��AOB��180����
���BCE����AOB-��ECD-��ACD��180��-90��-(90��-![]() )��
)��![]() ��
��
��3�������⣺![]() ����FCA-��DCA��
����FCA-��DCA��![]() (90��+30t)-30t��45��-15t
(90��+30t)-30t��45��-15t
![]() ����AC1D1+��AC1F1��30t+
����AC1D1+��AC1F1��30t+![]() (90����30t)��45��+15
(90����30t)��45��+15
��|![]() |��20�㣬
|��20�㣬
��|30t|��20�㣬
���t��![]() ��
��
�ʴ�Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��һ�ô�����BF��һ��б�£��½�Ϊ30�㣬ijʱ��̫����ֱ��б��BF��������A��Ӱ���䵽б���ϵĵ�D������֪BC=6m��BD=4m��������AC�ĸ߶ȣ������ȷ��0.1m���ο����ݣ� ![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��������֯����Ʒ�˵¡����������Ȼ��ÿ��ֻ��һ�������ij���мס��ҡ�������ѧ�����뾺ѡ����һ�ָ��ݡ�Ʒ�й淶������ѧϰ�淶�������������ˣ����ұ����ǵ��������˳ɼ�����λ���֣��ֱ������ַ�ʽ������ͳ�ƣ����±���ͼ1��


��1���뽫����ͼ1�еĿ�ȱ���ֲ���������
��2����ѡ�ĵڶ������ɱ����50λѧ������ͶƱ��ÿƱ��6�֣��ס��ҡ������˵ĵ�Ʊ�����ͼ2��û����ȨƱ��ÿ��ѧ��ֻ��ѡһ�ˣ���
��������Ʒ�й淶������ѧϰ�淶��������Ʊ��������Ե÷ְ�4:3:3�ı���ȷ�����ɼ���ͨ������˭���ᱻ��ѡΪУ����Ʒ�˵¡������꣮
�����涨��Ʊ���Է�ռ20����Ҫʹ��ѧ�����÷ֲ�����91�֣���Ʒ�й淶���ɼ����ܷ�����ռ������ȡֵ��ΧӦ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020�������ڼ䣬ij��˾Ϊ������Ӫ����������6̨���������������֣����мס������ֻ�����ѡ������ÿ�ֻ����ļ۸��ÿ̨�������������ֵ��������±���ʾ������Ԥ�㣬���ι�����������ʽ��ܳ���36��Ԫ��
��1�����ù�˾Ҫ������м��ֹ���?
��2������ù�˾������6̨�������������������ܵ���42�������ôΪ�˽�Լ�ʽ�Ӧѡ��ʲô���Ĺ���?
�� | �� | |
�۸���Ԫ/̨�� | 7 | 5 |
ÿ̨�ղ���������� | 10 | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ� ��
A.�������¼������ĸ���Ϊ0
B.����¼������ĸ���Ϊ ![]()
C.���ʺ�С���¼������ܷ���
D.Ͷ��һö�ʵؾ��ȵ�Ӳ��100�Σ����泯�ϵĴ���һ��Ϊ50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�١�ͼ�ڣ��ڸ�����һ�ž���ֽƬ����һ�������Σ��ס������˵��������£�
�ף��Ե�AΪԲ�ģ�AD��Ϊ�뾶��������AB�ڵ�E���Ե�DΪԲ�ģ�AD��Ϊ�뾶��������CD�ڵ�F������EF�����ı���AEFD��Ϊ����
�ң�����DAB��ƽ���ߣ���CD�ڵ�M��ͬ������ADC��ƽ���ߣ���AB�ڵ�N������MN�����ı���ADMN��Ϊ����


�������������������������������(����)
A.����ȷ���Ҵ���B.�ס��Ҿ���ȷ
C.����ȷ���״���D.�ס��Ҿ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڡ�ABC�У�AE��BF�ǽ�ƽ���ߣ������ཻ�ڵ�O��AD�Ǹߣ���BAC=50������C=70��������DAE����AOB�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
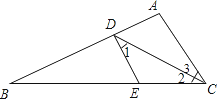
����Ŀ����ͼ����֪CDƽ�֡�ACB����1=��2��
��1����֤��DE��AC��
��2������3=30������B=25�������BDE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫƽ����ʽ��ʽ�ֽ�����ѧ�е�Ӧ�ã���ش��������⣺
��1����ʽ�ֽ⣺![]() _______��
_______��
��2����գ�
�ٵ�![]() ʱ������ʽ
ʱ������ʽ![]() _______��
_______��
�ڵ�![]() _______ʱ������ʽ
_______ʱ������ʽ![]() ��
��
�۴���ʽ![]() ����Сֵ��_______��
����Сֵ��_______��
��3����չ��Ӧ�ã���![]() ��
��![]() Ϊ��ֵʱ������ʽ
Ϊ��ֵʱ������ʽ![]() ����Сֵ������������Сֵ��
����Сֵ������������Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com