练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
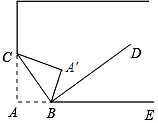
    2．如图，将书角斜折过去，使角顶点落在A′处，BC为折痕，∠A′BD=∠DBE，求∠CBD的度数．

    分析 根据角平分线的定义可得，∠CBD=∠CBA′+∠DBA′=$\frac{1}{2}$（∠A′BA+∠A′BE），又因为∠A′BA+∠A′BE=180°，由此即可解决问题．

    解答 解：由题意可知，∠ABC=∠A′BC，∠EBD=∠DBA′，
    ∴∠CBA′=$\frac{1}{2}$∠ABA′，∠A′BD=$\frac{1}{2}$∠A′BE，
    ∴∠CBD=∠CBA′+∠DBA′=$\frac{1}{2}$（∠A′BA+∠A′BE），
    ∵∠A′BA+∠A′BE=180°，
    ∴∠CBD=90°．

    点评 本题考查角平分线的定义，平角等知识，解题的关键是熟练掌握角平分线的定义，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

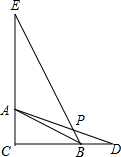    12．已知，Rt△ABC中∠C=90°，点D在边CB的延长线上，BD=AC，点E在边CA的延长线上，AE=CD，连接BE、AD交于点P，若BC=2BD=2，则PE=$\frac{{9\sqrt{5}}}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．已知一个三角形的三边长分别是4，6，x，若x的值为奇数，则x的取值有（　　）
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．两件商品都卖120元，其中一件赢利25%，另一件亏本20%，则两件商品卖出后（　　）
    A．赢利16元B．亏本16元C．赢利6元D．亏本6元

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

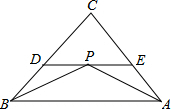    17．如图，△ABC中，∠ABC，∠CAB的平分线交于点P，过点P作DE∥AB，分别交BC、AC于点D、E．
    （1）如果∠C=80°，求∠BPA的度数．
    （2）求证：DE=BD+AE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，已知两同心圆，大圆的弦AB切小圆于M，若环形的面积为9π，则AB的长是6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，已知反比例函数y=$\frac{2}{x}$的图象上有一组点B1，B2，…Bn，它们的横坐标依次增加1，且点B1横坐标为1．“①，②，③…”分别表示如图所示的三角形的面积，记S1=①-②，S2=②-③，…，S1+S2+…+Sn=$\frac{n}{n+1}$（用含n的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：
    （1）若点（x1，y1），（x2，y2）在图象上，当x2＞x1＞0时，y2＞y1；
    （2）当x＜-1时，y＞0；
    （3）4a+2b+c＞0；
    （4）x=3是关于x方程ax2+bx+c=0的一个根，其中正确的个数为（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．计算：|-4|-（-1）8-cos45°=5-$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    同步练习册答案