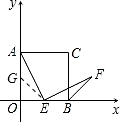
解:
(1)由题意得m=n时,AOBC是正方形.
如图,在OA上取点G,使AG=BE,
∵正方形OACB,OA=OB,
∴OG=OE.
∴∠EGO=∠GEO=

(180°-90°)=45°,从而∠AGE=90°+45°=135°.
由BF是外角平分线,得∠EBF=135°,
∴∠AGE=∠EBF.
∵∠AEF=90°,
∴∠FEB+∠AEO=90°.
在Rt△AEO中,∵∠EAO+∠AEO=90°,
∴∠EAO=∠FEB,
在△AGE和△EBF中
∵
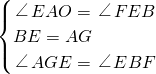
∴△AGE≌△EBF,
EF=AE.
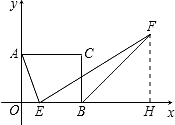
(2)假设存在点E,使EF=AE.设E(a,0).作FH⊥x轴于H,如图.
由(1)知∠EAO=∠FEH,于是Rt△AOE≌Rt△EHF.
∴FH=OE,EH=OA.
∴点F的纵坐标为a,即FH=a.
由BF是外角平分线,知∠FBH=45°,
∴BH=FH=a.
又由C(m,n)有OB=m,
∴BE=OB-OE=m-a,
∴EH=m-a+a=m.
又EH=OA=n,
∴m=n,这与已知m≠n相矛盾.
因此在边OB上不存在点E,使EF=AE成立.
(3)如(2)图,设E(a,0),FH=h,则EH=OH-OE=h+m-a.
由∠AEF=90°,∠EAO=∠FEH,得△AOE∽△EHF,
∴EF=(t+1)AE等价于FH=(t+1)OE,即h=(t+1)a,
且
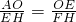
,即
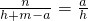
,
整理得nh=ah+am-a
2,
∴h=
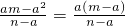
.
把h=(t+1)a代入得
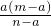
=(t+1)a,
即m-a=(t+1)(n-a).
而m=tn,因此tn-a=(t+1)(n-a).
化简得ta=n,解得a=
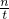
.
∵t>1,
∴
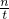
<n<m,
故E在OB边上.
∴当E在OB边上且离原点距离为
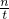
处时满足条件,此时E(
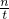
,0).
分析:(1)根据m=n,我们可得出四边形AOBC应该是个正方形.要证EF=AE,可通过构建全等三角形来实现,在OA上取点C,使AG=BE,则OG=OE.那么我们的目的就是证三角形ABE和EBF全等,这两个三角形中已知的条件只有AG=BE,我们发现∠AGE和∠EBF都是90+45=135°,而∠GAE和∠FEB都是∠AEO的余角,那么这两组对应角就相等,构成了三角形全等的条件,于是EF=AE了.
(2)可用反证法来求解,方法同(1)类似,也是通过构建全等三角形来求解.作FH⊥x轴于H,假设题目给出的条件成立,通过证明三角形AOE和EHF全等来得出线段相等,即AO=EH,OE=FH,根据FBH=45°,设E(a,0).那么FH=BH=OE=a,那么不难得出EH=EB+BH=OE+EB=m,又根据AO=EH,m=n,因此不存在点E.
(3)可根据相似三角形来得出线段之间的比例关系来求得.辅助线作法同(2),我们不难证得三角形AOE和FEH相似(根据同角的余角相等和一组直角即可得出相似),那么就能将EF=(t+1)AE转换为FH=(t+1)OE,根据相似我们还可得出关于AO、EH、OE、FH的比例关系,那么就能得出一个关于OE、FH、m、n的关系式,将这式子进行化简,即可得出OE与m、n的关系,便能求出E的坐标了.
点评:本题解题的关键是根据全等三角形的判定或相似三角形得出线段相等或成比例.

 解:
解: (180°-90°)=45°,从而∠AGE=90°+45°=135°.
(180°-90°)=45°,从而∠AGE=90°+45°=135°.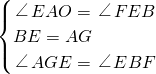

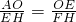 ,即
,即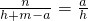 ,
,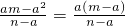 .
.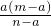 =(t+1)a,
=(t+1)a,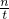 .
.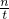 <n<m,
<n<m,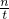 处时满足条件,此时E(
处时满足条件,此时E(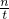 ,0).
,0).

 轻松暑假总复习系列答案
轻松暑假总复习系列答案 如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD. (2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是
(2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y= ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.