
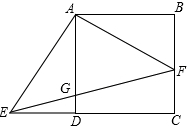
 如图,在正方形ABCD中,边长为1,F是边BC上一动点(点F与点B、点C均不重合),且AF⊥AE,AE交CD的延长线于点E,联结EF交AD于点G.
如图,在正方形ABCD中,边长为1,F是边BC上一动点(点F与点B、点C均不重合),且AF⊥AE,AE交CD的延长线于点E,联结EF交AD于点G.分析 (1)由正方形的性质,可得AB=AD,再根据已知和同角的余角相等得出可得出∠BAF=∠EAD,从而证明出△BAF≌△EAD,则BF=DE.再根据AD∥BC,推出 $\frac{DG}{FC}=\frac{BF}{EC}$,化为乘积式即可;
(2)由(1)可知△BAF≌△EAD,则AF=AE,所△AEF为等腰直角三角形,在Rt△ABF中,由勾股定理求得AF2=x2+1,然后由三角形的面积公式列出y与x之间的函数关系式即可;
(3)设BF=x,则FC=1-x,EC=1+x,由AF=FG,则∠FAG=∠FGA,再根据AD∥BC,推出△ABF∽△ECF.则 $\frac{BF}{AB}$=$\frac{FC}{EC}$,即 $\frac{x}{1}=\frac{1-x}{1+x}$.从而可求出x,舍去负根,从而求出BF的长.
解答 解:(1)证明:∵正方形ABCD,
∴AB=AD,∠ABC=∠ADE=90°,∠BAD=90°.
又∵AE⊥AF,
∴∠EAF=90°.
∴∠BAD=∠EAF,即∠BAF+∠FAD=∠EAD+∠DAF
∴∠BAF=∠EAD.
在△BAF和△EAD中,$\left\{\begin{array}{l}{∠EAD=∠BAF}\\{AD=AB}\\{∠ADE=∠ABF}\end{array}\right.$,
∴△BAF≌△EAD.
∴BF=DE.
∵AD∥BC,
∴$\frac{DG}{FC}=\frac{ED}{EC}$.
∴$\frac{DG}{FC}=\frac{BF}{EC}$.
∴BF•FC=DG•EC.
(2)∵△BAF≌△EAD,
∴AF=AE.
∵在Rt△ABF中,AF2=AB2+BF2,
∴AF2=1+x2.
∴y=$\frac{1}{2}AE•AF$=$\frac{1}{2}A{F}^{2}$=$\frac{1}{2}{x}^{2}+\frac{1}{2}$.
∴y与x之间的函数关系式为y=$\frac{1}{2}{x}^{2}+\frac{1}{2}$.
(3)存在.
理由:设BF=x,则FC=1-x,EC=1+x,
若AF=FG,则∠FAG=∠FGA
∵AD∥BC,
∴∠BFA=∠FAG,∠CFE=∠FGA.
∴∠BFA=∠CFE.
又∠ABF=∠ECF=90°,
∴△ABF∽△ECF.
∴$\frac{BF}{AB}=\frac{FC}{EC}$,即:$\frac{x}{1}=\frac{1-x}{1+x}$.
∴x2+2x-1=0.
解得:x1=$\sqrt{2}$-1,选x2=$-\sqrt{2}-1$(舍去).
∴BF=$\sqrt{2}-1$.
点评 本题考查了相似三角形的判定和性质、全等三角形的判定和性质以及正方形的性质、平行线分线段成比例定理.是中考压轴题,难度较大,证得△BAF≌△EAD是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 已知a、b为直角三角形两直角边,且a、b为一元二次方程:x2-(2k+1)x+k2+k+$\frac{1}{4}$=0的两根.
已知a、b为直角三角形两直角边,且a、b为一元二次方程:x2-(2k+1)x+k2+k+$\frac{1}{4}$=0的两根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| C | D | 总计 | |
| A | x吨 | 200-x | 200吨 |
| B | 240-x | x+60 | 300吨 |
| 总计 | 240吨 | 260吨 | 500吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,且AB=18,AC=12.
已知:如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,且AB=18,AC=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化单位:万人 | 0.16 | 0.08 | 0.04 | -0.04 | -0.08 | 0.02 | -0.12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com