
 如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=2,BC=4.P为线段BC上的
如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=2,BC=4.P为线段BC上的分析 作AM⊥PG于M.设BP=x.首先证明△APB≌△APM,在Rt△AMG中利用勾股定理列出方程即可解决问题.
解答 解:如图,作AM⊥PG于M.设BP=x.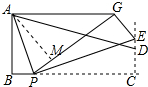
∵∠APE=90°,
∴∠APG+∠GPE=90°,∠APB+∠EPC=90°,
∵∠EPG=∠EPC,
∴∠BPA=∠APM,
∵AB⊥BP,AM⊥PG,
∴AB=AM=2,
在Rt△APB和Rt△APM中,
$\left\{\begin{array}{l}{PA=PA}\\{AB=AM}\end{array}\right.$,
∴△APB≌△APM,
∴PB=PM=x,
∵AG∥BC,
∴∠APB=∠PAG=∠APG,
∴AG=GP=PC=4-x,
在Rt△AMG中,∵AM2+MG2=AG2,
∴22+(4-2x)2=(4-x)2,
∴3x2-8x+4=0,
∴x=2或$\frac{2}{3}$,
∴PB=2或$\frac{2}{3}$,
故答案为$\frac{2}{3}$或2
点评 本题考查翻折变换、全等三角形的判定和性质、勾股定理等知识,教育的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
 如图,已知点A为反比例函数y=$\frac{k}{x}$的图象上任意一点,过点A作AB⊥x轴于B,若△ABO的面积为1,则k的值为( )
如图,已知点A为反比例函数y=$\frac{k}{x}$的图象上任意一点,过点A作AB⊥x轴于B,若△ABO的面积为1,则k的值为( )| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18cm | B. | 20 cm | C. | 24 cm | D. | 25cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\frac{1}{3}$ | B. | -$\frac{3}{10}$ | C. | $\frac{3}{10}$ | D. | -$\frac{10}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com