
分析 ①原式利用减法法则变形,计算即可得到结果;
②原式利用减法法则变形,结合后相加即可得到结果;
③原式从左到右依次计算即可得到结果;
④原式逆用乘法分配律计算即可得到结果;
⑤原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
⑥原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;
⑦原式利用乘法分配律计算即可得到结果;
⑧原式变形后,利用乘法分配律计算即可得到结果.
解答 解:①原式=8-10-2+5=13-12=1;
②原式=2$\frac{1}{7}$-3$\frac{1}{7}$-3$\frac{2}{3}$-5$\frac{1}{3}$=-1-9=-10;
③原式=-81×$\frac{4}{9}$×$\frac{4}{9}$×$\frac{1}{16}$=-1;
④原式=-$\frac{22}{7}$×(-7+26+2)=-$\frac{22}{7}$×21=-66;
⑤原式=16÷(-4)×$\frac{1}{4}$+1=-1+1=0;
⑥原式=-1-$\frac{1}{6}$×(-6)=-1+1=0;
⑦原式=-18+20-21=-19;
⑧原式=(-200+$\frac{1}{25}$)×5=-1000+$\frac{1}{5}$=-999$\frac{4}{5}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
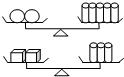 如图所示,第一个天平的两侧分别放2个球体和5个圆柱体,第二个天平的两侧分别放2个正方体和3个圆柱体,两个天平都平衡,则12个球体的质量等于( )个正方体的质量.
如图所示,第一个天平的两侧分别放2个球体和5个圆柱体,第二个天平的两侧分别放2个正方体和3个圆柱体,两个天平都平衡,则12个球体的质量等于( )个正方体的质量.| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地100千米.
甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地100千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com