

分析 (1)利用勾股定理和三角形ABC的面积的两种算法直接求解;
(2)平移到点D到AC时,点A到D的位置,根据平移的性质直接求解;
(3)根据题意画出满足条件的图形,根据勾股定理和等腰三角形的性质直接求解.
解答 解:(1)在Rt△ABC中,AC=15,BC=20,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=25,tan∠ABC=$\frac{AC}{BC}$=$\frac{3}{4}$
∵CD⊥AB,
∴CD=$\frac{AC×BC}{AB}$=12,
根据勾股定理得,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=9,
(2)如图1,
∵点E是点D关于AC的对称点,
∴DE⊥AC,AE=AD,
∵点E落在AC上,
∴点A落在点D位置,
由平移的性质,EF=AD=m,
(3)由(1)得,AE'=AD=9,
在Rt△AEC中,AC=15,
∴EC=$\sqrt{A{C}^{2}-A{E}^{2}}$=12,
①旋转的过程中,C'E'和线段BC相交,AB的延长线相交时,
如图2,
由旋转得,AC'=AC=15,∠CAE'=∠BAC',
∵∠AE'C'=∠C=90°,∠AFE'=∠PFC,
∴∠CAE'=∠CPF,
∴∠BAC'=∠CPF,
∵∠CPF=∠BPQ,
∴∠BAC'=∠BPQ,
∵△BPQ为等腰三角形,且∠CBQ是钝角,
∴BP=BQ,
∴∠BPQ=∠BQP,
∴∠BAC'=∠BQP,
∴C'Q=AC'=15,
在Rt△AE'Q中,AE'=AE=AD=9,E'Q=EC+C'Q=E'C'+AC'=12+15=27,
∴AQ=$\sqrt{AE{'}^{2}+E'{Q}^{2}}$=9$\sqrt{10}$,
②如图3,
∵△BPQ为等腰三角形,
∴∠PBQ=∠BPQ,
∵∠BPQ+∠E'FA=90°,∠E'AF+∠E'FA=90°,
∴∠E'AF=∠ABC,
∵tan∠ABC=$\frac{AC}{BC}$=$\frac{3}{4}$
∵tan∠E'AF=$\frac{E'F}{AE'}$=$\frac{E'F}{9}=\frac{3}{4}$,
∴E'F=$\frac{27}{4}$,
根据勾股定理得,AF=$\frac{45}{4}$,∴CF=AC-AF=15-$\frac{45}{4}$=$\frac{15}{4}$,
在Rt△CPF中,tan∠BPQ=$\frac{CF}{PC}=\frac{3}{4}$,∴PC=$\frac{4}{3}$CF=5,∴BP=BC+PC=25,PF=$\sqrt{P{C}^{2}+C{F}^{2}}$=$\frac{25}{4}$
∴PG=$\frac{1}{2}$BP=$\frac{25}{2}$,∵CF∥QG,∴$\frac{PF}{PQ}=\frac{PC}{PG}$,∴$\frac{\frac{25}{4}}{PQ}=\frac{5}{\frac{25}{2}}$,∴PQ=$\frac{125}{8}$,
∴AQ=AB-BQ=AB-PQ=$\frac{75}{8}$,
③如图4,
旋转的过程中,C'E'和线段BC,AB相交时,
Ⅰ、当∠BQP=∠PBQ时,
∵∠PBQ=∠AC'E',∠BQP=∠AQC',
∴∠AC'E'=∠AQC',
∴AQ=AC'=AC=15,
Ⅱ、当∠BPQ=∠BQP时,
∵∠BPQ=∠AC'E',
∴∠C'AQ=∠C'QA,
∴C'Q=C'A=15,
∴QE'=C'Q-C'E'=15-12=3,
根据勾股定理得,AQ=$\sqrt{AE{'}^{2}+E'{Q}^{2}}$=3$\sqrt{10}$,
即满足条件的AQ的长为9$\sqrt{10}$,$\frac{75}{8}$,15,3$\sqrt{10}$.
点评 .此题是几何变换综合题,主要考查了等腰三角形的性质,直角三角形的性质,解本题的关键是用等腰三角形的性质求AQ,根据题意画出图形是本题的难点.


科目:初中数学 来源: 题型:填空题
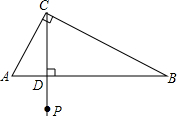 如图,在△ABC中,∠ACB=90°,∠B=30°,BC=6,CD为AB边上的高,点P为射线CD上一动点,当点P运动到使△ABP为等腰三角形时,BP的长度为4$\sqrt{3}$或6$\sqrt{2}$.
如图,在△ABC中,∠ACB=90°,∠B=30°,BC=6,CD为AB边上的高,点P为射线CD上一动点,当点P运动到使△ABP为等腰三角形时,BP的长度为4$\sqrt{3}$或6$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com