
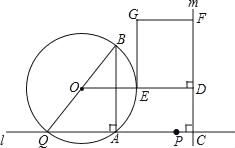
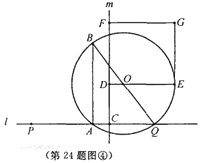
【题目】如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=![]() CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
(1)用关于x的代数式表示BQ,DF.
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).
【答案】(1)BQ=5x,FD=3x;(2)9;(3)①12或![]() 或3;②6
或3;②6 ![]() 或
或![]() .
.
【解析】试题分析:(1)根据Rt△ABQ中AQ:AB=3:4得出AQ=3x,AB=4x,BQ=5x,根据CD⊥m,l⊥m得出OD∥l,则OB=OQ,AH=BH=2x,则CD=2x,则FD=![]() CD=3x;(2)AP=AQ=3x PC=4 ∴CQ="6x+4" 作OM⊥AQ于点M(如图①)根据外接圆的性质得出∠BAQ=90°,则点O是BQ的中点,则QM=AM=
CD=3x;(2)AP=AQ=3x PC=4 ∴CQ="6x+4" 作OM⊥AQ于点M(如图①)根据外接圆的性质得出∠BAQ=90°,则点O是BQ的中点,则QM=AM=![]() x,则OD=MC=
x,则OD=MC=![]() x+4,OE=
x+4,OE=![]() x,ED=2x+4,根据矩形的面积求出x的值,从而的好粗AP的长度;(3)①当矩形为正方形时,则ED=FD,点P在点A的右侧时,画出图形得出2x+4=3x,得出x的值和AP的长度;点P在点A的左侧时,当点C在点Q右侧当 0<x<
x,ED=2x+4,根据矩形的面积求出x的值,从而的好粗AP的长度;(3)①当矩形为正方形时,则ED=FD,点P在点A的右侧时,画出图形得出2x+4=3x,得出x的值和AP的长度;点P在点A的左侧时,当点C在点Q右侧当 0<x<![]() 时,画出图形得出ED=4-7x,FD=3x,求出x的值和AP的长度;当
时,画出图形得出ED=4-7x,FD=3x,求出x的值和AP的长度;当![]() ≤x<
≤x<![]() 时, ED=7-4x,DF=3x,从而求出x的值;当点C在点Q左侧时,即x≥
时, ED=7-4x,DF=3x,从而求出x的值;当点C在点Q左侧时,即x≥![]() 画出图形可得:DE=7x-4,DF=3x,然后求出x的值和AP的长度;②、连结NQ,有点O到BN的弦心距为1得:NQ=2,当点N在AB的左侧时画出图形,过点B作BM⊥EG于点M,根据GM=x,BM=x得出∠GBM=45°,根据BM∥AQ,decubitusAI="AB=4x" ,IQ=x,NQ=
画出图形可得:DE=7x-4,DF=3x,然后求出x的值和AP的长度;②、连结NQ,有点O到BN的弦心距为1得:NQ=2,当点N在AB的左侧时画出图形,过点B作BM⊥EG于点M,根据GM=x,BM=x得出∠GBM=45°,根据BM∥AQ,decubitusAI="AB=4x" ,IQ=x,NQ=![]() =2,从而求出x的值,得出AP的长度;当点N在AB的右侧时,画出图形,然后利用同样的方法求出AP的长度.
=2,从而求出x的值,得出AP的长度;当点N在AB的右侧时,画出图形,然后利用同样的方法求出AP的长度.
试题解析:(1)在Rt△ABQ中,∵AQ:AB=3:4 ∴AQ=3x ∴AB=4x BQ=5x
又∵CD⊥m,l⊥m ∴OD∥l ∵OB=OQ ∴AH=BH=![]() AB=2x ∴CD=2x ∴FD=
AB=2x ∴CD=2x ∴FD=![]() CD=3x
CD=3x
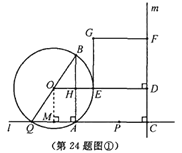
(2)∵AP=AQ=3x PC=4 ∴CQ=6x+4 作OM⊥AQ于点M(如图①) ∴OM∥AB
∵![]() O是△ABQ的外接圆 ∠BAQ=90° ∴点O是BQ的中点 ∴QM=AM=
O是△ABQ的外接圆 ∠BAQ=90° ∴点O是BQ的中点 ∴QM=AM=![]() x ∴OD=MC=
x ∴OD=MC=![]() x+4
x+4
∴OE=![]() BQ=
BQ=![]() x ∴ED=2x+4 ∴矩形DEGF的面积=DF·DE=3x(2x+4)=90
x ∴ED=2x+4 ∴矩形DEGF的面积=DF·DE=3x(2x+4)=90
∴![]() =-5(舍去)
=-5(舍去)![]() =3 ∴AP=3x=9
=3 ∴AP=3x=9
(3)①若矩形DEGF是正方形 则ED=FD
I、点P在点A的右侧时(如图①) ∴2x+4=3x,解得:x=4 ∴AP=3x=12
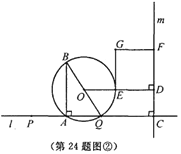
II、点P在点A的左侧时 当点C在点Q右侧 0<x<![]() 时(如图②) ∵ED=4-7x,FD=3x
时(如图②) ∵ED=4-7x,FD=3x
∴4-7x=3x 解得:x=![]() ∴AP=
∴AP=![]()
当![]() ≤x<
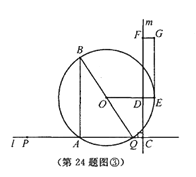
≤x<![]() 时(如图③) ED=7-4x,DF=3x ∴7-4x=3x 解得:x=1(舍去)
时(如图③) ED=7-4x,DF=3x ∴7-4x=3x 解得:x=1(舍去)
当点C在点Q左侧时,即x≥![]() (如图④) DE=7x-4 DF=3x ∴7x-4=3x 解得:x=1 ∴AP=3
(如图④) DE=7x-4 DF=3x ∴7x-4=3x 解得:x=1 ∴AP=3
综上所述:当AP为12或![]() 或3时,矩形DEGF是正方形
或3时,矩形DEGF是正方形
②、AP的长为6![]() 或
或![]()
连结NQ,有点O到BN的弦心距为1得:NQ=2
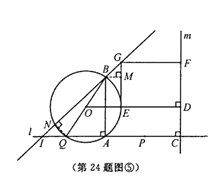
当点N在AB的左侧时(如图⑤) 过点B作BM⊥EG于点M ∵GM=x,BM=x ∴∠GBM=45°
∴BM∥AQ,∴AI=AB=4x ∴IQ=x ∴NQ=![]() =2 ∴x=2
=2 ∴x=2![]() ∴AP=6
∴AP=6![]()
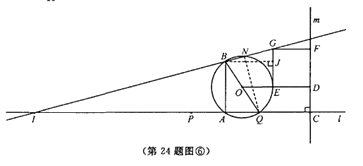
当点N在AB的右侧时(如图⑥),过点B作BJ⊥GE于点J ∵GJ=x,BJ=4x ∴tan∠GBJ=![]()
∴AI=16x ∴QI=19x ∴NQ=![]() =2 ∴x=
=2 ∴x=![]() ∴AP=
∴AP=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
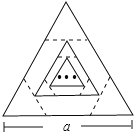
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,两半径为r的等圆⊙O1和⊙O2相交于M,N两点,且⊙O2过点O1.过M点作直线AB垂直于MN,分别交⊙O1和⊙O2于A,B两点,连接NA,NB.
(1)猜想点O2与⊙O1有什么位置关系,并给出证明;
(2)猜想△NAB的形状,并给出证明;
(3)如图2,若过M的点所在的直线AB不垂直于MN,且点A,B在点M的两侧,那么(2)中的结论是否成立,若成立请给出证明.
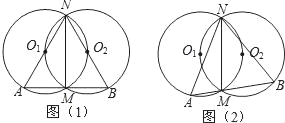
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P是∠ABC内一点.
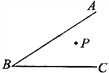
(1)画图:①过点P画BC的垂线,垂足为D;②过点P画BC的平行线交AB于点E,过点P画AB的平行线交BC于点F.
(2)∠EPF等于∠B吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一节快到了,甲、乙两家旅行社为了吸引更多的顾客,分别提出了赴某地旅游的团体优惠方法,甲旅行社的优惠方法是:买4张全票,其余人按半价优惠;乙旅行社的优惠方法是:一律按7折优惠,已知两家旅行社的原价均为每人100元。(旅游人数超过4人)
(1)分别表示出甲旅行社收费y1 ,乙旅行社收费y2与旅游人数x的函数关系式.
(2)就参加旅游的人数讨论哪家旅行社的收费更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县实施新课程改革后,学生的自主字习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调査,并将调査结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调査结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)本次调查中,张老师一共调査了 名同学,其中C类女生有 名,D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D为等腰直角△ABC内一点,∠ACB=90°,AD=BD,∠BAD=30°,E为AD延长线上的一点,且CE=CA,若点M在DE上,且DC=DM.则下列结论中:①∠ADB=120°;②△ADC≌△BDC;③线段DC所在的直线垂直平分线AB;④ME=BD;正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com