
分析 (1)设每台空调、电风扇的进货价分别为x,y元,进而利用购进8台空调和20台电风扇共需17400元,购进10台空调和30台电风扇共需22500元,得出方程组求解即可;
(2)利用空调标价为2500元/台,电风扇标价为250元/台.若商场购进空调和电风扇共60台,并全部打八折出售,分别表示出其价格,进而得出函数关系式即可;
(3)利用这批空调和电风扇的进货价不超过45300元,求出a的取值范围,再根据一次函数的性质进行计算即可.
解答 解:(1)设每台空调、电风扇的进货价分别为x,y元,由题意可得:
$\left\{\begin{array}{l}{8x+20y=17400}\\{10x+30y=22500}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1800}\\{y=150}\end{array}\right.$.
所以每台空调进货价为1800元,每台电风扇进货价为150元;
(2)根据题意可得:
w=(2500×0.8-1800)a+(250×0.8-150)(60-a)
=150a+3000,
(3)由题可得:1800a+150(60-a)≤45300
解得a≤22
∵a取正整数,一次函数w随a的增大而增大
∴当a=22时,获得的利润最高,最高利润w=150×22+3000=6300(元)
点评 本题主要考查了一函数应用以及二元一次方程组的应用等知识,根据题意得出正确的函数关系式是解题的关键.解题时注意,在求最大或最小值时,一般需要结合一次函数的性质进行分析判断.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
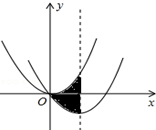 如图,在平面直角坐标系中,抛物线y=$\frac{1}{3}$x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{8}{3}$,则a、b的值分别为( )
如图,在平面直角坐标系中,抛物线y=$\frac{1}{3}$x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{8}{3}$,则a、b的值分别为( )| A. | $\frac{1}{3}$,$\frac{4}{3}$ | B. | $\frac{1}{3}$,-$\frac{8}{3}$ | C. | $\frac{1}{3}$,-$\frac{4}{3}$ | D. | -$\frac{1}{3}$,$\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>4 | B. | x≥-2且x≠4 | C. | x>-2且x≠4 | D. | x≠4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为10.
如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com