
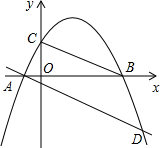
 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B,与y轴交于点C,将直线BC平移,使其经过点A,且与抛物线交于点D,求证:∠BDA=45°.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B,与y轴交于点C,将直线BC平移,使其经过点A,且与抛物线交于点D,求证:∠BDA=45°. 分析 如图,过点B作BE⊥AD于点E.由二次函数图象上点的坐标特征求得点A、B、C的坐标,然后利用待定系数法和二次函数与一次函数交点得到点D的坐标,所以通过证明△BED为等腰三角形即可证得结论.
解答 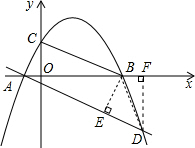 证明:如图,作DF⊥x轴于点F,作BE⊥AD于点E.
证明:如图,作DF⊥x轴于点F,作BE⊥AD于点E.
y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-$\frac{1}{2}$(x-4)(x+1),则A(-1,0),B(4,0),
令x=0,则y=2,
故C(0,2).
易求直线BC的解析式为:y=-$\frac{1}{2}$x+2,
∵将直线BC平移,使其经过点A,且与抛物线交于点D,
∴设直线AD的解析式为:y=-$\frac{1}{2}$x+b.
把点C的坐标代入,得
b=-$\frac{1}{2}$,
则直线AD的解析式为y=-$\frac{1}{2}$x-$\frac{1}{2}$.
则$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2}\\{y=-\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=5}\\{y=-3}\end{array}\right.$(舍去正值),
则D(5,-3).
∴$\frac{1}{2}$AB×3=$\frac{1}{2}$AD•BE,AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=3$\sqrt{5}$,
易得h=BE=$\sqrt{5}$.
在直角△ABE中,AE=$\sqrt{A{B}^{2}-{h}^{2}}$=2$\sqrt{5}$,
∴DE=AD-AE=$\sqrt{5}$,
∴h=DE且BE⊥AD,
∴∠BDA=45°.
点评 本题考查了抛物线与x轴的交点.解题时,要熟悉抛物线与一次函数图象交点的求法,等腰直角三角形的判定与性质.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$,60° | B. | 1,45° | C. | $\sqrt{3}$,60° | D. | $\frac{\sqrt{3}}{3}$,30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
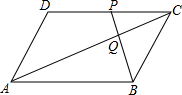 如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.
如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
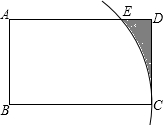 如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交边AD于点E,AB=4,BC=8,则图中弧$\widehat{CE}$,线段DE,CD围成的阴影部分的面积为32-8$\sqrt{3}$-$\frac{4π}{3}$.
如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交边AD于点E,AB=4,BC=8,则图中弧$\widehat{CE}$,线段DE,CD围成的阴影部分的面积为32-8$\sqrt{3}$-$\frac{4π}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
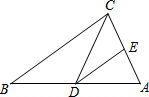 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )| A. | △ADE∽△ABC | B. | △ADE∽△ACD | C. | △DEC∽△CDB | D. | △ADE∽△DCB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 悬挂物体的质量x/kg | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 弹簧的长度l/cm | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15.5 | 16 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2和$\frac{1}{2}$ | B. | -2和$\frac{1}{2}$ | C. | 2$\frac{3}{8}$和-2.375 | D. | +(-2)和-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com