
已知, 点P是∠MON的平分线上的一动点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON于点B,且使∠APB+∠MON=180°.
(1)利用图1,求证:PA=PB;
(2)如图2,若点![]() 是
是![]() 与
与![]() 的交点,当
的交点,当![]() 时,求PB与PC的比值;
时,求PB与PC的比值;
(3)若∠MON=60°,OB=2,射线AP交ON于点![]() ,且满足且
,且满足且![]() ,请借助图3补全图形,并求
,请借助图3补全图形,并求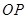 的长.
的长.
(1)(2)
(3)
解:(1)在OB上截取OD=OA,连接PD,
∵OP平分∠MON,
∴∠MOP=∠NOP.
又∵OA=OD,OP=OP,
∴△AOP≌△DOP. ……………1分
∴PA=PD,∠1=∠2.
∵∠APB+∠MON=180°,
∴∠1+∠3=180°.
∵∠2+∠4=180°,
∴∠3=∠4.
∴PD=PB.
∴PA=PB. …………… 2分
(2)
∵PA=PB,
∴∠3=∠4.
∵∠1+∠2+∠APB=180°,且∠3+∠4+∠APB=180°,
∴∠1+∠2=∠3+∠4.
∴∠2=∠4.
∵∠5=∠5,
∴△PBC∽△POB.
∴![]() . …………… 5分
. …………… 5分
(3)作BE⊥OP交OP于E,
∵∠AOB=600,且OP平分∠MON,
∴∠1=∠2=30°.
∵∠AOB+∠APB=180°,
∴∠APB=120°.
∵PA=PB,
∴∠5=∠6=30°.
∵∠3+∠4=∠7,
∴∠3+∠4=∠7=(180°![]() 30°)÷2=75°.
30°)÷2=75°.
∵在Rt△OBE中,∠3=600,OB=2
∴∠4=150,OE=![]() ,BE=1
,BE=1
∴∠4+∠5=450,
∴在Rt△BPE中,EP=BE=1
∴OP=![]() …………… 8分
…………… 8分
解析:略


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
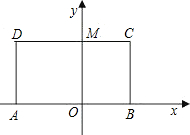 如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3.
如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3.查看答案和解析>>
科目:初中数学 来源: 题型:
 3)是反比例函数图象上的点:
3)是反比例函数图象上的点:查看答案和解析>>
科目:初中数学 来源: 题型:
 25、已知;如图,AB是半圆O的直径,弦CD∥AB,直线CM、DN分别切半圆于点C、D,且分别和直线AB相交于点M、N.
25、已知;如图,AB是半圆O的直径,弦CD∥AB,直线CM、DN分别切半圆于点C、D,且分别和直线AB相交于点M、N.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知平面直角坐标系xOy(如图),一次函数y=
已知平面直角坐标系xOy(如图),一次函数y=| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
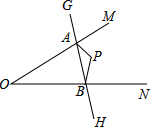 如图,已知∠MON=45°,P是∠MON内的一点,点G、H分别是P点关于MO、NO的对称点,GH与OM,ON分别相交于点A,B.已知GH=5cm,则△PAB的周长是
如图,已知∠MON=45°,P是∠MON内的一点,点G、H分别是P点关于MO、NO的对称点,GH与OM,ON分别相交于点A,B.已知GH=5cm,则△PAB的周长是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com