
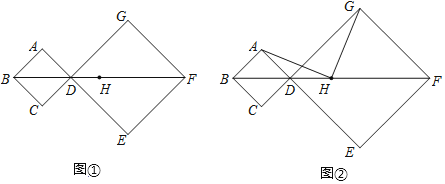
【题目】已知:在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
(1)如图①,若AB=1,DG=2,求BH的长;
(2)如图②,连接AH、GH,求证:AH=GH且AH⊥GH.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)先根据勾股定理得出AB,DG,进而求出BF,即可得出结论;
(2)先判断△ABH≌△MFH,进而判断出△ADG≌△MFG.即可判断出△AGM为等腰直角三角形,即可得出结论;
(1)解:∵正方形中ABCD和正方形DEFG,
∴△ABD,△GDF为等腰直角三角形.
∵AB=1,DG=2,
∴由勾股定理得BD=![]() ,DF=
,DF=![]() .
.
∵B、D、F共线,
∴BF=![]() .
.
∵H是BF的中点,
∴BH=![]() BF=
BF=![]() ;
;
(2)如图1,延长AH交EF于点M,连接AG,GM,
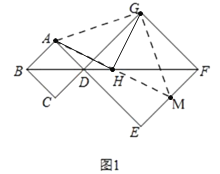
∵正方形中ABCD和正方形DEFG且B、D、F共线,
∴AB∥EF.
∴∠ABH=∠MFH.
又∵BH=FH,∠AHB=∠MHF,
∴△ABH≌△MFH.
∴AH=MH,AB=MF.
∵AB=AD,
∴AD=MF.
∵DG=FG,∠ADG=∠MFG=90°,
∴△ADG≌△MFG.
∴∠AGD=∠MGF,AG=MG.
又∵∠DGM+∠MGF=90°,
∴∠AGD+∠DGM=90°.
∴△AGM为等腰直角三角形.
∵AH=MH,
∴AH=GH,AH⊥GH.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:
早在2011年9月25日,北京故宫博物院就开始尝试网络预售门票,2011年全年网络售票仅占1.68%.2012年至2014年,全年网络售票占比都在2%左右.2015年全年网络售票占17.33%,2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日,首次实现全部网上售票.与此同时,网络购票也采用了“人性化”的服务方式,为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后,在北京故宫博物院的精细化管理下,观众可以更自主地安排自己的行程计划,获得更美好的文化空间和参观体验.
材料二:
以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.
年度 | 2013 | 2014 | 2015 | 2016 | 2017 |
参观人数(人次) | 7 450 000 | 7 630 000 | 7 290 000 | 7 550 000 | 8 060 000 |
年增长率(%) | 38.7 | 2.4 | -4.5 | 3.6 | 6.8 |

他还注意到了如下的一则新闻:2018年3月8日,中国国家博物馆官方微博发文,宣布取消纸质门票,观众持身份证预约即可参观. 国博正在建设智慧国家博物馆,同时馆方工作人员担心的是:“虽然有故宫免(纸质)票的经验在前,但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票,他遵守预约的程度是不一样的.但(国博)免费就有可能约了不来,挤占资源,所以难度其实不一样.” 尽管如此,国博仍将积极采取技术和服务升级,希望带给观众一个更完美的体验方式.
根据以上信息解决下列问题:
(1)补全以下两个统计图;
(2)请你预估2018年中国国家博物馆的参观人数,并说明你的预估理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具专柜从太原市小商品批发市场购进一批胶带,每个进价0.5元.调查发现,当销售价为0.8元时,每月可售出500个;如果售价每降低0.05元,那么平均每月可多售出200个.
(1)当降价0.2元时,平均每月销售胶带______个;
(2)摊主要想平均每月赢利180元,且尽可能让利与顾客,应该如何定价?
(3)在(2)的条件下,每个胶带的利润率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
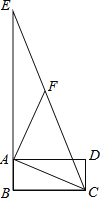
【题目】在探究“尺规三等分角”这个数学命题中,利用了如图,该图中,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是(________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
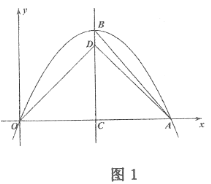
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,对称轴分别交抛物线和
,对称轴分别交抛物线和![]() 轴于点
轴于点![]() 和点
和点![]() ,以
,以![]() 为底边向上作等腰
为底边向上作等腰![]() .
.
(1)![]() ______;
______;![]() ______(用含
______(用含![]() 的代数式表示);
的代数式表示);
(2)如图1,当![]() 时,连接
时,连接![]() ,求
,求![]() 的值;
的值;
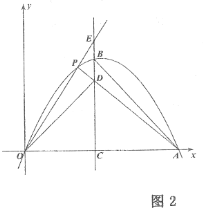
(3)点![]() 是抛物线
是抛物线![]() 段上任意一点,连接
段上任意一点,连接![]() 和
和![]() ,延长
,延长![]() 交对称轴于点
交对称轴于点![]() ,如图2,若
,如图2,若![]() ,
,![]() ,
,![]() 三点在一条直线上,当
三点在一条直线上,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是抛物线![]() 对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.
对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月22日深圳地铁10号线华南城站试运行,预计今年6月正式开通.在地铁的建设中,某段轨道的铺设若由甲乙两工程队合做,12天可以完成,共需工程费用27720元;已知乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.

(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com