
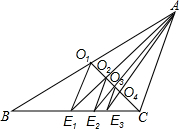
 如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En.则OnEn=$\frac{1}{n+1}$AC.(用含n的代数式表示)
如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En.则OnEn=$\frac{1}{n+1}$AC.(用含n的代数式表示) 分析 先根据平行相似证明△BO1E1∽△BAC,列比例式得:$\frac{{O}_{1}{E}_{1}}{AC}=\frac{B{O}_{1}}{AB}$,再根据中点的定义得:BO1=$\frac{1}{2}$AB,
所以O1E1=$\frac{1}{2}AC$,同理可得:O2E2=$\frac{1}{3}$AC,O3E3=$\frac{1}{4}$AC,…,OnEn=$\frac{1}{n+1}$AC.
解答 解∵O1E1∥AC,
∴△BO1E1∽△BAC,
∴$\frac{{O}_{1}{E}_{1}}{AC}=\frac{B{O}_{1}}{AB}$,
∵O1是AB的中点,
∴BO1=$\frac{1}{2}$AB,
∴$\frac{{O}_{1}{E}_{1}}{AC}=\frac{1}{2}$,
∴O1E1=$\frac{1}{2}AC$,
∵O1E1∥AC,
∴△O1E1O2∽△CAO2,
∴$\frac{{O}_{1}{E}_{1}}{AC}=\frac{{E}_{1}{O}_{2}}{{E}_{1}A}$=$\frac{1}{2}$,
∴$\frac{{E}_{1}{O}_{2}}{{E}_{1}A}$=$\frac{1}{3}$,
∵O2E2∥AC,
∴△E1O2E2∽△E1AC,
∴$\frac{{O}_{2}{E}_{2}}{AC}=\frac{{E}_{1}{O}_{2}}{{E}_{1}A}$=$\frac{1}{3}$,
∴O2E2=$\frac{1}{3}$AC,
同理得:$\frac{{O}_{3}{E}_{3}}{AC}=\frac{{E}_{2}{O}_{3}}{{E}_{2}A}$=$\frac{1}{4}$,
O3E3=$\frac{1}{4}$AC,
…
∴OnEn=$\frac{1}{n+1}$AC,
故答案为:$\frac{1}{n+1}$.
点评 本题考查了三角形相似的性质和判定,熟练掌握平行相似的判定是本题的关键,也可以利用中位线定理得出第一个结论.


科目:初中数学 来源: 题型:填空题
 如图所示.(V球=$\frac{4}{3}$πr3)
如图所示.(V球=$\frac{4}{3}$πr3)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
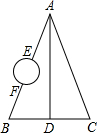 如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=DC=l km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km,则建造的斜拉桥长至少为1.1km.
如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=DC=l km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km,则建造的斜拉桥长至少为1.1km.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
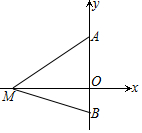 如图,在直角坐标系中,点A(0,a2-a)和点B(0,-3a-5)在y轴上,点M在x轴负半轴上,S△ABM=6.当线段OM最长时,点M的坐标为(-3,0).
如图,在直角坐标系中,点A(0,a2-a)和点B(0,-3a-5)在y轴上,点M在x轴负半轴上,S△ABM=6.当线段OM最长时,点M的坐标为(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com