
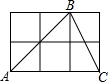
 如图,六个正方形组成一个矩形,A,B,C均在格点上,则∠ABC的正切值为3.
如图,六个正方形组成一个矩形,A,B,C均在格点上,则∠ABC的正切值为3. 分析 首先过点A作AD⊥BC于点D,利用三角形的面积求得AD的长,再利用勾股定理求得BD的长,继而求得答案.
解答 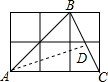 解:过点A作AD⊥BC于点D,
解:过点A作AD⊥BC于点D,
∵S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×3×2,BC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴AD=$\frac{6}{\sqrt{5}}$=$\frac{6\sqrt{5}}{5}$,
∵AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\frac{2\sqrt{5}}{5}$,
∴tan∠ABC=$\frac{AD}{BD}$=$\frac{\frac{6\sqrt{5}}{5}}{\frac{2\sqrt{5}}{5}}$=3.
故答案为:3.
点评 此题考查了矩形的性质、勾股定理以及三角函数等知识.注意准确作出辅助线是解此题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -1 | 0 | 2 | 4 | … |
| y1 | … | 0 | 1 | 3 | 5 | … |
| x | … | -1 | 1 | 3 | 4 | … |
| y2 | … | 0 | -4 | 0 | 5 | … |
| A. | x<-1 | B. | x>4 | C. | -1<x<4 | D. | x<-1或x>4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6S}}{6}$ | B. | $\frac{\sqrt{5S}}{5}$ | C. | $\frac{\sqrt{6S}}{2}$ | D. | $\sqrt{6S}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方B点共四圈,已知易拉罐底面周长是12cm,高是20cm,那么所需彩带最短的是( )
如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方B点共四圈,已知易拉罐底面周长是12cm,高是20cm,那么所需彩带最短的是( )| A. | 13cm | B. | 4$\sqrt{61}$cm | C. | 4$\sqrt{34}$cm | D. | 52cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com