
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx��2 ��x�ύ�ڵ�A����1��0����B��4��0������M��N��x���ϣ���N�ڵ�M�Ҳ࣬MN=2����MNΪֱ�DZ�����������ֱ��������CMN����CMN=90�㣮���M�ĺ�����Ϊm��
��1������������������Ӧ�ĺ�����ϵʽ��
��2�����C��������������ʱm��ֵ��
��3�����߶�CN�Ƶ�N��ʱ����ת90��õ���Ӧ�߶�DN��
�ٵ���D�����������ߵĶԳ�����ʱ�����D�����꣮
����DNΪֱ�DZ�������ֱ��������DNE������E�����������ߵĶԳ�����ʱ��ֱ��д�����з���������mֵ��
���ο���ʽ��������y=ax2+bx+c��a��0���Ķ�������Ϊ ��
��
��1��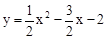 ��
��
��2��m��ֵΪ ��
��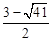 ��
��
��3���ٵ�D������Ϊ��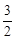 ����2����
����2����
��m��ֵΪm=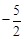 ��m=
��m= ��m=
��m=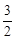 ��m=
��m=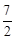 ��
��
���������������1����A����1��0����B��4��0��������������y=ax2+bx��2�����ô���ϵ����������������ߵĽ���ʽ��
��������y=ax2+bx��2������A����1��0����B��4��0����
�� �����
�����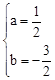 ��
��
������������Ӧ�ĺ�����ϵʽΪ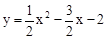 ��
��
��2�����ݵ���ֱ�������ε����������C������Ϊ��m��2�����ٽ�C���������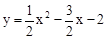 ���������m��ֵ��
���������m��ֵ��
�ߡ�CMN�ǵ���ֱ�������Σ���CMN=90�㣬��CM=MN=2�����C������Ϊ��m��2����
�ߵ�C��m��2�����������ϣ���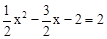 ��
��
���m1= ��m2=
��m2=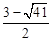 ��
��
���C��������������ʱ��m��ֵΪ ��
��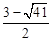 ��
��
��3����������ת�����ʵó���D������Ϊ��m����2�������ݶ��κ������������������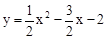 �ĶԳ���Ϊֱ��x=
�ĶԳ���Ϊֱ��x=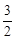 ��Ȼ����ݵ�D��ֱ��x=
��Ȼ����ݵ�D��ֱ��x=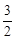 �ϣ����������D�����ꡣ
�ϣ����������D�����ꡣ
����ͼ����DNΪֱ�DZ�������ֱ��������DNE��E���λ�������������
���E����E1��λ��ʱ��
�ߵ�D������Ϊ��m����2����MN=ME1=2����N������Ϊ��m+2��0����
���E1�ģ�m��2��0����
�ߵ�E1��������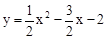 �ĶԳ���x=
�ĶԳ���x=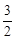 �ϣ�
�ϣ�
��m��2=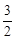 �����m=
�����m=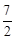 ��
��
���E����E2��λ��ʱ��
�ߵ�D������Ϊ��m����2������N������Ϊ��m+2��0����
���E2�ģ�m+2����4����
�ߵ�E2��������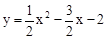 �ĶԳ���x=
�ĶԳ���x=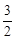 �ϣ���m+2=
�ϣ���m+2=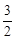 �����m=
�����m= ��
��
���E����E3��λ��ʱ��
�ߵ�D������Ϊ��m����2�������E3�ģ�m��2����
�ߵ�E3��������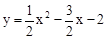 �ĶԳ���x=
�ĶԳ���x=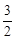 �ϣ���m=
�ϣ���m=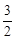 ��
��
���E����E4��λ��ʱ��
�ߵ�D������Ϊ��m����2������N������Ϊ��m+2��0�������E4�ģ�m+4����2����
�ߵ�E4��������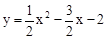 �ĶԳ���x=
�ĶԳ���x=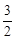 �ϣ���m+4=
�ϣ���m+4=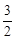 �����m=
�����m=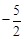 ��
��
���Ͽ�֪������E�����������ߵĶԳ�����ʱ�����з���������m��ֵΪm=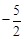 ��m=
��m= ��m=
��m=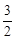 ��m=
��m=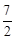 ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪���κ�����ͼ����A��6��0����B����2��0���͵�C��0����8����
��1����ö��κ����Ľ���ʽ��
��2����ö��κ���ͼ��Ķ���ΪM������KΪx���ϵĶ��㣬����KCM���ܳ���Сʱ����K������Ϊ�� ����
��3������AC����������P��Qͬʱ�ӵ�O���������е�P��ÿ��3����λ���ȵ��ٶ�������OAC��O��A��C��·���˶�����Q��ÿ��8����λ���ȵ��ٶ�������OCA��O��C��A��·���˶�����P��Q��������ʱ�����Ƕ�ֹͣ�˶�����P��Qͬʱ�ӵ�O����t��ʱ����OPQ�����ΪS��
������P��Q�������˶������У��Ƿ����PQ��OC�������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
�������S����t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
����S0�Ǣ��к���S�����ֵ��ֱ��д��S0��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��2013���Ĵ�����12�֣���ͼ�����κ���y=ax2+bx+c��ͼ��Ķ���C������Ϊ��0����2������x����A��B���㣬����A����1��0����ֱ��l��x=m��m��1����x�ύ��D��
��1������κ����Ľ���ʽ��B�����ꣻ
��2����ֱ��l���ҵ�P��P�ڵ�һ���ޣ���ʹ����P��D��BΪ���������������B��C��OΪ��������������ƣ����P�����꣨�ú�m�Ĵ���ʽ��ʾ����
��3���ڣ�2�������������£������������Ƿ���ڵ�һ�����ڵĵ�Q��ʹ��BPQ����PΪֱ�Ƕ���ĵ���ֱ�������Σ�������ڣ��������Q�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��2013���Ĵ��㰲10�֣���ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c����A��B��C���㣬��֪��A����3��0����B��0��3����C��1��0����
��1����������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ�����������һ���㣬�������A��B�غϣ�������P��x��Ĵ��ߣ�����ΪF����ֱ��AB�ڵ�E����PD��AB�ڵ�D��
�ٶ���P��ʲôλ��ʱ����PDE���ܳ���������ʱP������ꣻ
������PA����APΪ����ͼʾһ���������APMN�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮������M��Nǡ�����������߶Գ�����ʱ�������Ӧ��P������꣮������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c��y���ڵ�C��0��4�����Գ���x=2��x�ύ�ڵ�D������ΪM����DM=OC+OD��
��1����������ߵĽ���ʽ��
��2�����P��x��y���ǵ�һ�����ڸ��������ϵ�һ�����㣬��PCD�����ΪS����S����x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3���ڣ�2���������£���������P��ֱ��PE��y�ύ�ڵ�E���Ƿ������O��P��EΪ��������������OPDȫ�ȣ������ڣ������ֱ��PE�Ľ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��������y=x2+bx+c��x�ύ��A����1��0����B��3��0�����㣬��y���ڵ�E��
��1����������ߵĽ���ʽ��
��2����ֱ��y=x+1�������߽���A��D���㣬��y�ύ�ڵ�F������DE�����DEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��������y=��x2+4��x�ύ��A��B���㣬��y�ύ��C�㣬��P���������ϵ�һ���������ڵ�һ���ޣ�����P��x��Ĵ��ߣ�����ΪD����ֱ��BC�ڵ�E��
��1�����A��B��C�������ֱ��BC�Ľ���ʽ��
��2�����ODE��������ֵ����Ӧ�ĵ�E�����ꣻ
��3���Ƿ�����Ե�P��O��DΪ��������������OAC���ƣ������ڣ��������P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ1����֪A��3��0����B��4��4����ԭ��O��0��0����������y=ax2+bx+c ��a��0���ϣ�
��1���������ߵĽ���ʽ��
��2����ֱ��OB����ƽ��m����λ���Ⱥõ���ֱ����������ֻ��һ������D����m��ֵ����D�����꣮
��3����ͼ2������N���������ϣ��ҡ�NBO=��ABO�����ڣ�2���������£�������������POD�ס�NOB�ĵ�P�����꣨��P��O��D�ֱ����N��O��B��Ӧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
��֪����������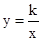 ��ͼ��P����1��2���������������ͼ��λ�ڣ� ��
��ͼ��P����1��2���������������ͼ��λ�ڣ� ��
| A���ڶ��������� | B����һ�������� |
| C�������������� | D���ڶ��������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com