
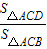 是否为一定值?若是定值,请求出其值;若不是定值,请说明理由.
是否为一定值?若是定值,请求出其值;若不是定值,请说明理由.
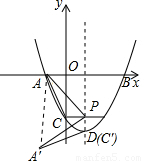 ,
, ×4×3a=6a,
×4×3a=6a, ×1×3a+
×1×3a+ (3a+4a)×1-
(3a+4a)×1- ×2×4a=a,
×2×4a=a,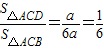 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2009年湖北省武汉市新洲区初中毕业年级数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年湖北省武汉市新洲区初中毕业年级数学试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2010年江西省中考数学模拟试卷(4)(解析版) 题型:解答题
| 甲品牌 | 乙品牌 | ||||
| 型号 | A | B | C | D | E |
| 价格(元) | 200 | 170 | 130 | 120 | 100 |
查看答案和解析>>
科目:初中数学 来源:2009年湖北省武汉市新洲区初中毕业年级数学试卷(解析版) 题型:解答题
 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com