
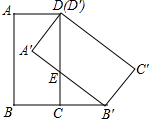
 ��ͼ���ھ���ABCD�У�BC=1��������ABCD�Ƶ�D��ʱ����ת45�㣬�õ�����A��B��C��D�䣬��B��ǡ������BC���ӳ����ϣ���A��B�佻��CD�ڵ�E��
��ͼ���ھ���ABCD�У�BC=1��������ABCD�Ƶ�D��ʱ����ת45�㣬�õ�����A��B��C��D�䣬��B��ǡ������BC���ӳ����ϣ���A��B�佻��CD�ڵ�E������ ��1���ɾ��ε����ʺ���ת�������жϳ���DBB���ǵ��������Σ�
��2�������μ��㣬�ɾ��ε�������ת�������ȼ����S��A��D��G��S�ı���D��GEF���ɣ�
��3�����ɾ��ε����ʺ���ת�����ʱ�ʾ����ص��߶Σ����ñ���ʽ$\frac{AD��}{A��M}=\frac{D��M}{A��M}$�����㼴�ɣ�
��� ֤������1����ͼ�٣�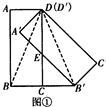
����DB��DB�䣬
���ı���ABCD�Ǿ��Σ�
���BCD=90�㣬
��DC��BB�䣬
����ת�У�DB=DB�䣬
��B��C=BC��
��2����ͼ�ڣ�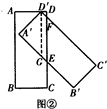
��0��t��1-$\frac{\sqrt{2}}{2}$ʱ����D��G��DC����A��B����G��
���ı���A��B��C��D���Ǿ��Σ�
��A��B���D��C��
���ı���D��GEF��ƽ���ı��Σ�
����ת�С�A��D��G=45�㣬
��A��D��=1��
��S��A��D��G=$\frac{1}{2}$��A��D��2=$\frac{1}{2}$��1=$\frac{1}{2}$��D��G=$\sqrt{2}$��
���˶�ʱ��Ϊt��
��DD��=t��
��S�ı���D��GEF=D��G��DD��=$\sqrt{2}$t��
��S=S��A��D��G+S�ı���D��GEF=$\frac{1}{2}$+$\sqrt{2}$t��
��t=1ʱ����ͼ�ۣ�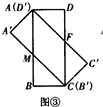
���ı���ABCD��A��B���D���Ǿ��Σ�
���ı���AMCF��ƽ���ı��Σ�
��S=AM��AD=$\sqrt{2}$A��D���AD=$\sqrt{2}$��1��1=$\sqrt{2}$��
��1+$\frac{\sqrt{2}}{2}$��t��2ʱ����ͼ�ܣ�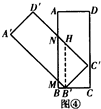
��B����B��M��AB��
ͬ�����ı���NMB��H��ƽ���ı��Σ�
��MN=B��H=$\sqrt{2}$B��C��=$\sqrt{2}$
�˶�ʱ��Ϊt��
��BB��=2-t��
��S=S��B��C��M+S�ı���NMB��H
=$\frac{1}{2}$��B��C��2+MN��BB��
=$\frac{1}{2}$��1+$\sqrt{2}$��2-t��
=$\frac{1}{2}$+2$\sqrt{2}$-$\sqrt{2}$t��
��3��
��A�����AB�ĶԳƵ������F��
��A��F��AB��
���ı���ABCDΪ���Σ�
��AD��AB��
��A��F��AD��
��ֱ��DF�����A��B��C��D��ı�ƽ��
����ͼ�ݣ�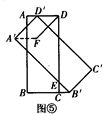
��DF��A��D��ʱ���ı���A��FDD����ƽ���ı��Σ�
��A��F=DD��=t��
��AD��=1-t��
�ߵ�A����F����AB�Գƣ�
��A��M=FM=$\frac{t}{2}$��
�ߡ�AD��M=��MA��F=45�㣬
��A��M=$\frac{\sqrt{2}}{2}$t��
��D��M=A��D��-A��M=1-$\frac{\sqrt{2}}{2}$t��
��AD��A��F��
��$\frac{AD��}{A��M}=\frac{D��M}{A��M}$��
��$\frac{1-t}{\frac{t}{2}}=\frac{1-\frac{\sqrt{2}}{2}t}{\frac{\sqrt{2}}{2}t}$��
��t=2-$\sqrt{2}$��
����ͼ�ޣ�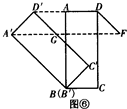
��DF��D��C��ʱ���ı���D��GFD��ƽ���ı��Σ�
��GF=DD��=t��
��A��G=$\sqrt{2}$A��D��=$\sqrt{2}$��
��A��F=A��G+GF=$\sqrt{2}$+t��
��A��F=2��t-1+$\frac{\sqrt{2}}{2}$��=2t-2+$\sqrt{2}$��
��$\sqrt{2}$+t=2t-2+$\sqrt{2}$��
��t=2��
����ֱ��DF�����A��B��C��D��ı�ƽ��ʱt��ֵΪ2-$\sqrt{2}$��2��
���� �����Ǽ��α任�ۺ��⣬��Ҫ�����˾��ε����ʣ���ת�����ʣ�����������ļ��㣬����������ʾ���߶��ǽӱ���Ĺؼ����ѵ��Ƿֶ���������ʽ�ͷ������t��ֵ��


 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��0 | B�� | x��1 | C�� | x��1��x��-1 | D�� | x��1��x��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com