
【题目】探究:如图,直线 AB、BC、AC 两两相交,交点分别为点 A、B、C,点 D 在线段 AB 上,过点 D 作 DE∥BC 交 AC 于点 E,过点 E 作 EF∥AB 交 BC 于点 F.若∠ABC=40°,求∠DEF 的度数. 请将下面的解答过程补充完整,并填空(理由或数学式)

解:∵DE∥BC,( )
∴∠DEF= .( )
∵EF∥AB,
∴ =∠ABC.( )
∴∠DEF=∠ABC.( )
∵∠ABC=40°,
∴∠DEF= °.
科目:初中数学 来源: 题型:
【题目】如图1,数轴上的点A,B.C依次表示数-2,x,4.某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点B,发现点A对齐刻度1.8cm,点C对齐刻度5.4cm.
(1)AC= 个单位长度;由图可知数轴上的一个单位长度对应刻度尺上的 cm;数轴上的点B表示数 ;

(2)已知T是数轴上一点(不与点A、点B、点C重合),点P表示的数是t,点P是线段BT的三等分点,且TP=2BP.
①如图3,当-2<t<4时,试试猜想线段CT与AP的数量关系,并说明理由;
②若|2BT-3AP|=1,请直接写出所有满足条件的t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明过程,并在括号内填上依据.
如图,点E在AB上,点F在CD上,∠1=∠2,∠B=∠C,求证AB∥CD.
证明:∵∠1=∠2(已知),∠1=∠4( ),
∴∠2= (等量代换),
∴ ∥BF( ),
∴∠3=∠ ( ).
又∵∠B=∠C(已知),
∴∠3=∠B( ),
∴AB∥CD( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实验课上,王老师让大家用矩形纸片折出菱形.小华同学的操作步骤是:
(1)如图①,将矩形ABCD沿着对角线BD折叠;
(2)如图②,将图①中的△A’BF沿BF折叠得到△A’’BF;
(3)如图③,将图②中的△CDF沿DF折叠得到△C’DF;
(4)将图③展开得到图④,其中BD、BE、DF为折叠过程中产生的折痕.

试解答下列问题:
(1)证明图④中的四边形BEDF为菱形;
(2)在图④中,若BC=8,CD=4,求菱形BEDF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节,某玩具超市设立了一个可以自由转动且只有铅笔和文具盒两个版块的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )
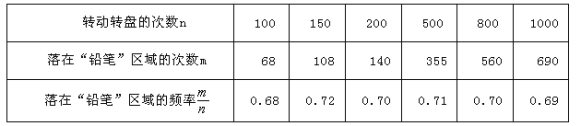

A.当![]() 很大时,估计指针落在“铅笔”区域的频率大约是0.70
很大时,估计指针落在“铅笔”区域的频率大约是0.70
B.假如你去转动转盘一次,获得铅笔的概率大约是0.70
C.如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D.转动转盘10次,一定有3次获得文具盒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南京某中学为了迎接世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:

请结合图表完成下列各题:
(1)求表中a的值:
(2)请把频数分布直方图补充完整:
(3)若测试成绩不低于90分的同学可以获得世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”?
查看答案和解析>>
科目:初中数学 来源: 题型:
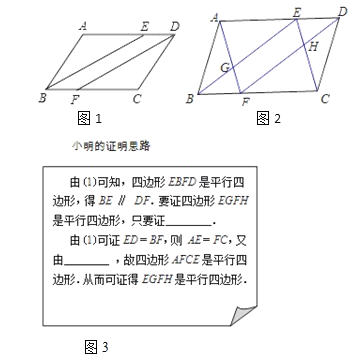
【题目】如图1,ABCD中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)如图2,小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图3)中补全他的证明思路,再在答题纸上写出规范的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题一:如图①,已知AC=160km,甲,乙两人分别从相距30km的A,B两地同时出发到C地.若甲的速度为80km/h,乙的速度为60km/h,设乙行驶时间为x(h),两车之间距离为y(km).
(1)当甲追上乙时,x= .
(2)请用x的代数式表示y.
问题二:如图②,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(3)分针OD指向圆周上的点的速度为每分钟转动 km,时针OE指向圆周上的点的速度为每分钟转动 °;
(4)若从2:00起计时,求几分钟后分针与时针第一次重合?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com