
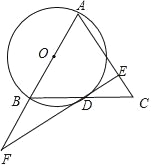
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E,交AB延长线于点F.
(1)求证:BD=CD;
(2)求证:DC2=CEAC;
(3)当AC=5,BC=6时,求DF的长.
【答案】(1)详见解析;(2)详见解析;(3)DF=![]() .
.
【解析】
(1)先判断出AD⊥BC,即可得出结论;
(2)先判断出OD∥AC,进而判断出∠CED=∠ODE,判断出△CDE∽△CAD,即可得出结论;
(3)先求出OD,再求出CD=3,进而求出CE,AE,DE,再判断出![]() ,即可得出结论.
,即可得出结论.
(1)连接AD,

∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD;
(2)连接OD,
∵DE是⊙O的切线,
∴∠ODE=90°,
由(1)知,BD=CD,
∵OA=OB,
∴OD∥AC,
∴∠CED=∠ODE=90°=∠ADC,
∵∠C=∠C,
∴△CDE∽△CAD,
∴![]() ,
,
∴CD2=CEAC;
(3)∵AB=AC=5,
由(1)知,∠ADB=90°,OA=OB,
∴OD=![]() AB=
AB=![]() ,
,
由(1)知,CD=![]() BC=3,
BC=3,
由(2)知,CD2=CEAC,
∵AC=5,
∴CE=![]() ,
,
∴AE=AC-CE=5-![]() =
=![]() ,
,
在Rt△CDE中,根据勾股定理得,DE=![]() ,
,
由(2)知,OD∥AC,
∴![]() ,
,
∴ ,
,
∴DF=![]() .
.


科目:初中数学 来源: 题型:
【题目】创新需要每个人的参与,就拿小华来说,为了解决晒衣服的,聪明的他想到了一个好办法,在家宽敞的院内地面![]() 上立两根等长的立柱
上立两根等长的立柱![]() 、
、![]() (均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线
(均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线![]() ,如图
,如图![]() ,已知立柱
,已知立柱![]() 米,
米, ![]() 米.
米.
(1)求绳子最低点离地面的距离;
(2)为了防止衣服碰到地面,小华在离![]() 为
为![]() 米的位置处用一根垂直于地面的立柱
米的位置处用一根垂直于地面的立柱![]() 撑起绳子 (如图2),使左边抛物线
撑起绳子 (如图2),使左边抛物线![]() 的最低点距
的最低点距![]() 为
为![]() 米,离地面
米,离地面![]() 米,求
米,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
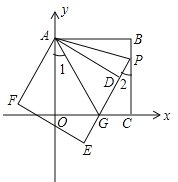
【题目】边长相等的两个正方形ABCO、ADEF如图摆放,正方形ABCO的边OA、OC在坐标轴上,ED交线段OC于点G,ED的延长线交线段BC于点P,连AG,已知OA长为![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,AG=2,求点G的坐标;
,AG=2,求点G的坐标;
(3)在(2)条件下,在直线PE上找点M,使以M、A、G为顶点的三角形是等腰三角形,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
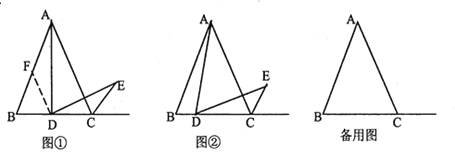
【题目】(1)(问题情境)小明遇到这样一个问题:
如图①,已知![]() 是等边三角形,点
是等边三角形,点![]() 为
为![]() 边上中点,
边上中点,![]() ,
,![]() 交等边三角形外角平分线
交等边三角形外角平分线![]() 所在的直线于点
所在的直线于点![]() ,试探究
,试探究![]() 与
与![]() 的数量关系.
的数量关系.
小明发现:过![]() 作
作![]() ,交
,交![]() 于
于![]() ,构造全等三角形,经推理论证问题得到解决.请直接写出
,构造全等三角形,经推理论证问题得到解决.请直接写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(2)(类比探究)
如图②,当![]() 是线段
是线段![]() 上(除
上(除![]() 外)任意一点时(其他条件不变)试猜想
外)任意一点时(其他条件不变)试猜想![]() 与
与![]() 的数量关系并证明你的结论.
的数量关系并证明你的结论.
(3)(拓展应用)
当![]() 是线段
是线段![]() 上延长线上,且满足
上延长线上,且满足![]() (其他条件不变)时,请判断
(其他条件不变)时,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的网格纸中,每个小正方形的边长都为1,动点
的网格纸中,每个小正方形的边长都为1,动点![]() ,
,![]() 分别从点
分别从点![]() ,点
,点![]() 同时出发向右移动,点
同时出发向右移动,点![]() 的运动速度为每秒2个单位,点
的运动速度为每秒2个单位,点![]() 的运动速度为每秒1个单位,当点
的运动速度为每秒1个单位,当点![]() 运动到点
运动到点![]() 时,两个点同时停止运动.
时,两个点同时停止运动.

(1)当运动时间![]() 为3秒时,请在网格纸图中画出线段
为3秒时,请在网格纸图中画出线段![]() ,并求其长度.
,并求其长度.
(2)在动点![]() ,
,![]() 运动的过程中,若
运动的过程中,若![]() 是以
是以![]() 为腰的等腰三角形,求相应的时刻
为腰的等腰三角形,求相应的时刻![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
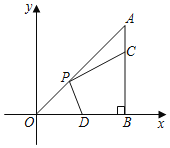
【题目】如图,在Rt△ABO中,∠OBA=90°,A(8,8),点C在边AB上,且![]() ,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )
,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )
A.(2,2)B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
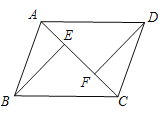
【题目】如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“流感”,某学校在休息日用“药熏”消毒法对教室进行消毒.已知药物释放过程中,室内每立方米的含药量y(毫克)与时间x(时)成正比例;药物释放结束后,y与x成反比例;如图所示,根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数解析式;
(2)据测定,当药物释放结束后,每立方米的含药量降至0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多长时间,学生才能进入教室?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com