
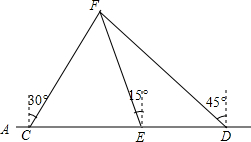
 如图,在东西方向的海岸线AB上,有C、D两艘巡逻船,现均收到故障船F的求救信号,已知C、D两船相距50($\sqrt{2}$+$\sqrt{6}$)海里,船F在船C的北偏东30°方向上,船F在船D的西北方向上,海岸线AB上有一观测点E,测得船F正好在观测点E的北偏西15°方向上.
如图,在东西方向的海岸线AB上,有C、D两艘巡逻船,现均收到故障船F的求救信号,已知C、D两船相距50($\sqrt{2}$+$\sqrt{6}$)海里,船F在船C的北偏东30°方向上,船F在船D的西北方向上,海岸线AB上有一观测点E,测得船F正好在观测点E的北偏西15°方向上.分析 (1)如图,作EG⊥CF,FH⊥CD,解直角三角形得到FH=CH•tan60°=$\sqrt{3}$x,FH=DH=$\sqrt{3}$x,求得CH+DH=x+$\sqrt{3}$x=50($\sqrt{2}$+$\sqrt{6}$),于是得到结论;
(2)设CG=y,则GF=GE=$\sqrt{3}$y,于是得到CF=y+$\sqrt{3}$y=100$\sqrt{2}$,求得CE=2y=100($\sqrt{6}$-$\sqrt{2}$),得到GE=$\sqrt{3}$CG=$\sqrt{3}$×50($\sqrt{6}$-$\sqrt{2}$)≈103海里,于是得到结论.
解答 解:(1)如图,作EG⊥CF,FH⊥CD, 由题意得:∠CDF=45°,∠FCD=60°,
由题意得:∠CDF=45°,∠FCD=60°,
设CH=x海里,
在Rt△CHF中,FH=CH•tan60°=$\sqrt{3}$x海里;
在Rt△DFH中,FH=DH=$\sqrt{3}$x海里,
∴CH+DH=x+$\sqrt{3}$x=50($\sqrt{2}$+$\sqrt{6}$),
解得:x=50$\sqrt{2}$,
∴CF=2x=100$\sqrt{2}$,FH=50$\sqrt{6}$海里,
∴DF=$\sqrt{2}$FH=100$\sqrt{3}$海里.
答:F与C之间的距离是100$\sqrt{2}$海里,F与D之间的距离是100$\sqrt{3}$海里;
(2)作EG⊥CF,设CG=y,则GF=GE=$\sqrt{3}$y,
∴CF=y+$\sqrt{3}$y=100$\sqrt{2}$,
解得:y=50($\sqrt{6}$-$\sqrt{2}$),
∴CE=2y=100($\sqrt{6}$-$\sqrt{2}$),
GE=$\sqrt{3}$CG=$\sqrt{3}$×50($\sqrt{6}$-$\sqrt{2}$)≈103海里,
∵103<100$\sqrt{3}$,
所以巡逻船C沿直线CF去弯救船F,在去营救的途中有触暗礁危险.
点评 本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形并选择合适的边角关系解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根,k为正整数.
已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根,k为正整数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com