
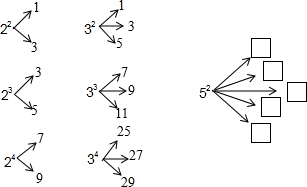
分析 根据已知中22=1+3,32=1+3+5,42=1+3+5+7,我们易归纳出n2=1+3+5+…+(2n-1);进而给出52的表达式,同样根据23=3+5,33=7+9+11,43=13+15+17+19,…n3分裂最小的数是n(n-1)+1,我们易归纳出43应该是73的分解中最小的数,进而得到答案.
解答 解:由22=1+3
32=1+3+5
42=1+3+5+7
…
n2=1+3+5+…+(2n-1);
则52=1+3+5+7+9“分裂”中最大的数是9;
从23起,k3的分解规律恰为数列3,5,7,9,
若干连续项之和,23为前两项和,
33为接下来三项和,
…
43=6×7+1
43是73的分解中最小的数,
∴m=7.
故答案为:9,7.
点评 此题考查数字的变化规律,(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
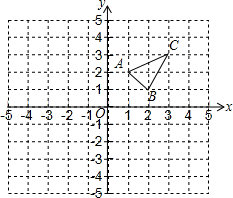 △ABC在平面直角坐标系中的位置如图所示,
△ABC在平面直角坐标系中的位置如图所示,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,港口A在观测站O的正东方向,某船从港口A出发,沿北偏东15°方向航行2km到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则观测站O距港口A的距离(即OA的长)为( )
如图,港口A在观测站O的正东方向,某船从港口A出发,沿北偏东15°方向航行2km到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则观测站O距港口A的距离(即OA的长)为( )| A. | $\sqrt{2}$km | B. | 2km | C. | 2$\sqrt{2}$km | D. | 4$\sqrt{2}$km |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com