
如图1,已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
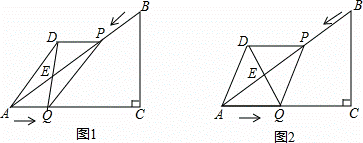
(1)用含有t的代数式表示AE= 5﹣t .
(2)当t为何值时,平行四边形AQPD为矩形.
(3)如图2,当t为何值时,平行四边形AQPD为菱形.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
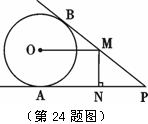
如图,PA,PB分别与⊙O相切于点A,B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM = AN;
(2)若⊙O的半径R = 3,PA = 9,求OM的长.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
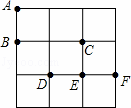
在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是 ;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率是 (用树状图或列表法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
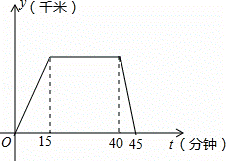
如图是王老师去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法正确的是( )
|
| A. | 王老师去时所用的时间少于回家的时间 |
|
| B. | 王老师在公园锻炼了40分钟 |
|
| C. | 王老师去时走上坡路,回家时走下坡路 |
|
| D. | 王老师去时速度比回家时的速度慢 |
查看答案和解析>>
科目:初中数学 来源: 题型:
国庆节期间,电器市场火爆.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
| 类 别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1 800 | 1 500 |
| 售价(元/台) | 2 000 | 1 600 |
计划购进电视机和洗衣机共100台,商店最多可筹集资金161 800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其他费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获 得利润最多?并求出最多利润.(利润=售价-进价)
得利润最多?并求出最多利润.(利润=售价-进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com