
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
【答案】
(1)
证明:连接OD,
∵AD平分∠BAC,
∴∠DAE=∠DAB,
∵OA=OD,∴∠ODA=∠DAO,
∴∠ODA=∠DAE,
∴OD∥AE,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O切线
(2)
解:过点O作OF⊥AC于点F,

∴AF=CF=3,
∴OF= ![]() =
= ![]() =4.
=4.
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED是矩形,
∴DE=OF=4.
【解析】(1)连接OD,欲证明DE是⊙O的切线,只要证明OD⊥DE即可.(2)过点O作OF⊥AC于点F,只要证明四边形OFED是矩形即可得到DE=OF,在RT△AOF中利用勾股定理求出OF即可.本题考查切线的判定、矩形的判定和性质、垂径定理、勾股定理等知识,解题的关键是记住切线的判定方法,学会添加常用辅助线,属于基础题,中考常考题型.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;

(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;

(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )

A. 正方形 B. 菱形 C. 矩形 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
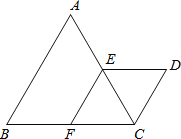
【题目】如图,△ABC与△CDE都是等边三角形,点E、F分别为AC、BC的中点。
(1) 求证:四边形EFCD是菱形;(2)如果AB=10,求D、F两点间的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知:如图1,直线AB∥CD,点E是AB、CD之间的一点,连接BE、DE得到∠BED.
求证:∠BED =∠B+∠D.
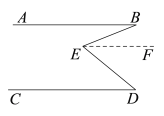 图1
图1
小冰是这样做的:
证明:过点E作EF∥AB,则有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF +∠FED =∠B+∠D.
即∠BED=∠B+∠D.
请利用材料中的结论,完成下面的问题:
已知:直线 AB∥CD,直线MN分别与AB、CD交于点E、F.
(1)如图2,∠BEF和∠EFD的平分线交于点G.猜想∠G的度数,并证明你的猜想;
(2)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2.求证:∠FG1 E+∠G2=180°.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
(1)求证:AE=AF;
(2)求证:BE= ![]() (AB+AC).
(AB+AC).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com