
【题目】如图1,四边形ABGC内接于⊙O,GA平分∠BGC.
(1)求证:AB=AC;
(2)如图2,过点A作AD∥BG交CG于点D,连接BD交线段AG于点W,若∠BAG+∠CAD=∠AWB,求证:BD=BG;
(3)在(2)的条件下,若CD=5,BD=16,求WG的长.

【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)由GA平分∠BGC可得∠AGB=∠AGC,然后跟胡圆周角定理证明即可;
(2)设∠AGB=∠AGC=x,证得∠BAG+∠CAD=180°﹣3x=∠AWB,则∠BGD=∠BDG=2x,可得出结论BD=BG;
(3)延长GC,使CK=BG=16,连接AK.根据SAS证明△ABG≌△ACK,可得∠K=∠AGB=∠AGC,得出AG=AK,过点A作AN⊥GK于点N,过点B作BH⊥DG于点H,设HD=GH=a,可得出DN=NG﹣DG=![]() ,证明△ADN∽△BDH,得出比例线段求出a=6,求出AG的长,证明△AWD∽△BWG,得出
,证明△ADN∽△BDH,得出比例线段求出a=6,求出AG的长,证明△AWD∽△BWG,得出![]() ,可求出WG.
,可求出WG.
(1)证明:∵GA平分∠BGC,
∴∠AGB=∠AGC,
∴弧AB=弧AC,
∴AB=AC;
(2)证明:设∠AGB=∠AGC=x,
∵四边形ABCD内接于圆O,
∴∠BAC=180°﹣2x,
∵AD//BG,
∴∠AGB=∠DAG,
∴∠AGD=∠DAG=x,
∴∠BAG+∠CAD=180°﹣3x=∠AWB,
∵∠AWB=∠AGB+∠DBG,
∴∠DBG=180°﹣3x﹣x=180°﹣4x,
∴∠BDG=180°﹣2x﹣(180°﹣4x)=2x,
∴∠BGD=∠BDG=2x,
∴BD=BG;
(3)解:如图2,延长GC,使CK=BG=BD=16,连接AK.
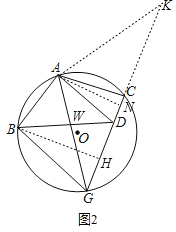
∵AB=AC,∠ACK=∠ABG,
∴△ABG≌△ACK(SAS),
∴∠K=∠AGB=∠AGC=x,
∴AG=AK,
过点A作AN⊥GK于点N,过点B作BH⊥DG于点H,
设HD=GH=a,
∵CD=5,
∴GK=2a+5+16=2a+21,
∵AG=AK,AN⊥GK,
∴![]() ,
,
∴DN=NG﹣DG=![]() ,
,
∵∠AND=∠BHD,∠ADC=∠BGD=∠BDH,
∴△ADN∽△BDH,
∴![]() ,
,
∵∠AGD=∠DAG,
∴AD=GD=2a,
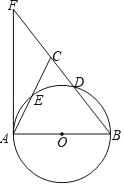
∴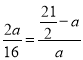 ,
,
∴a2+8a﹣84=0,
解得a1=6,a2=﹣14(舍去),
∴AD=12,
∴在Rt△AND中,![]() ,
,
在Rt△AGN中,AG=![]() =
= =6
=6![]() ,
,
∵AD//BG,
∴△AWD∽△BWG,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】定义:如果函数C:![]() (
(![]() )的图象经过点(m,n)、(-m,-n),那么我们称函数C为对称点函数,这对点叫做对称点函数的友好点.
)的图象经过点(m,n)、(-m,-n),那么我们称函数C为对称点函数,这对点叫做对称点函数的友好点.
例如:函数![]() 经过点(1,2)、(-1,-2),则函数
经过点(1,2)、(-1,-2),则函数![]() 是对称点函数,点(1,2)、(-1,-2)叫做对称点函数的友好点.
是对称点函数,点(1,2)、(-1,-2)叫做对称点函数的友好点.
(1)填空:对称点函数![]() 一个友好点是(3,3),则b= ,c= ;
一个友好点是(3,3),则b= ,c= ;
(2)对称点函数![]() 一个友好点是(2b,n),当2b≤x≤2时,此函数的最大值为
一个友好点是(2b,n),当2b≤x≤2时,此函数的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() =4,求b的值;
=4,求b的值;
(3)对称点函数![]() (
(![]() )的友好点是M、N(点M在点N的上方),函数图象与y轴交于点A.把线段AM绕原点O顺时针旋转90°,得到它的对应线段A′M′.若线段A′M′与该函数的图象有且只有一个公共点时,结合函数图象,直接写出a的取值范围.
)的友好点是M、N(点M在点N的上方),函数图象与y轴交于点A.把线段AM绕原点O顺时针旋转90°,得到它的对应线段A′M′.若线段A′M′与该函数的图象有且只有一个公共点时,结合函数图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D是⊙O上一点,点E是AC的中点,过点A作⊙O的切线交BD的延长线于点F.连接AE并延长交BF于点C.
(1)求证:AB=BC;
(2)如果AB=5,tan∠FAC=![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
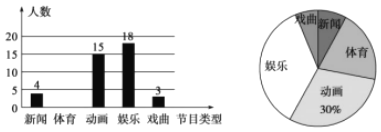
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电影公司随机收集了2000部电影的有关数据,经分类整理得到如表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
好评率 |
|
|
|
|
|
|
注:好评率是指一类电影中获得好评的部数与该类电影的部数的比值.
![]() 如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
![]() 电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化
电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化![]() 假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加
假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加![]() ,哪类电影的好评率减少
,哪类电影的好评率减少![]() ,可使改变投资策略后总的好评率达到最大?
,可使改变投资策略后总的好评率达到最大?
答:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点F在边BC上,过点F作EF⊥BC,且FE=FC(CE<CB),连接CE、AE,点G是AE的中点,连接FG.
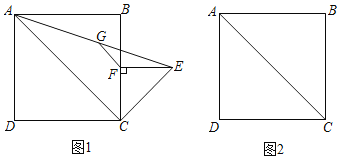
(1)用等式表示线段BF与FG的数量关系是 ;
(2)将图1中的△CEF绕点C按逆时针旋转,使△CEF的顶点F恰好在正方形ABCD的对角线AC上,点G仍是AE的中点,连接FG、DF.
①在图2中,依据题意补全图形;
②求证:DF=![]() FG.
FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
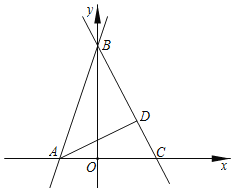
【题目】已知如图,直线AB交x轴于点A,交y轴于点B,AB=![]() ,tan∠BAO=3.
,tan∠BAO=3.
(1)求直线AB的解析式;
(2)直线y=kx+b经过点B交x轴交于点C,且∠ABC=45°,AD⊥BC于点D.动点P从点C出发,沿CB方向以每秒![]() 个单位长度的速度向终点B运动,运动时间为t,设△ADP的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围.
个单位长度的速度向终点B运动,运动时间为t,设△ADP的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围.
(3)在(2)的条件下,点P在线段BD上,点F在线段AB上,∠APC=∠FPB,连接AP,过点F作FG⊥AP于点G,交AD于点H,若DP=DH,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
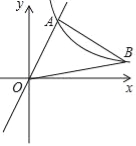
【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则k的值为 .
,∠AOB=∠OBA=45°,则k的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com