
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:填空题
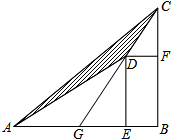 如图,D为△ABC内的一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为24.
如图,D为△ABC内的一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为24.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
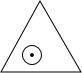 如图,一个半径为1的圆形纸片在边长为a(a≥2$\sqrt{3}$)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
如图,一个半径为1的圆形纸片在边长为a(a≥2$\sqrt{3}$)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )| A. | $\frac{π}{3}$ | B. | $\frac{3\sqrt{3}-π}{3}$ | C. | 3$\sqrt{3}$-π | D. | 不能求出具体值 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
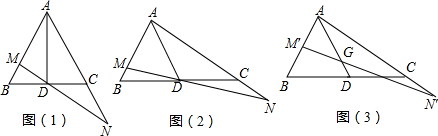
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
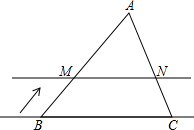 如图,在△ABC中,AB=7,AC=$\sqrt{17}$,BC=8,线段BC所在直线以每秒2个单位的速度沿BA方向运动,并始终保持与原位置平行.该直线与AB、AC分别交于点M、N,记x秒时,并设△AMN中MN边上的高为y.试写出y关于x的函数关系式y=-2x+$\sqrt{13}$,自变量x的取值范围是0<x<$\sqrt{13}$.
如图,在△ABC中,AB=7,AC=$\sqrt{17}$,BC=8,线段BC所在直线以每秒2个单位的速度沿BA方向运动,并始终保持与原位置平行.该直线与AB、AC分别交于点M、N,记x秒时,并设△AMN中MN边上的高为y.试写出y关于x的函数关系式y=-2x+$\sqrt{13}$,自变量x的取值范围是0<x<$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一个边长为a的正方形材料上截取一扇形,围成母线长为a的圆锥.
在一个边长为a的正方形材料上截取一扇形,围成母线长为a的圆锥.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com