
分析 设2、3月份的月增长率为x,则2月份产值为500(1+x)万元,3月份的产值为500(1+x)2万元.根据第一季度的总产值为1820万元,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
解答 解:设2、3月份的月增长率为x,则2月份产值为500(1+x)万元,3月份的产值为500(1+x)2万元.
根据题意得:500+500(1+x)+500(1+x)2=1820,
整理得:25x2+75x-16=0,
解得:x1=0.2=20%,x2=-3.2(舍去).
答:2、3月份的月增长率为20%.
点评 本题考查了一元二次方程的应用,由1、2、3月份的总产值,列出关于x的一元二次方程是解题的关键.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,对角线AC、BD相交于点O,且AO=CO,BO=DO,要使四边形ABCD为矩形,则需添加的条件为∠DAB=90°(填一个即可).
如图,在四边形ABCD中,对角线AC、BD相交于点O,且AO=CO,BO=DO,要使四边形ABCD为矩形,则需添加的条件为∠DAB=90°(填一个即可).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
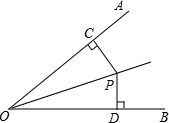 如图,OP为∠AOB内的一条射线,PC⊥OA,PD⊥OB,垂足分别是C,D,请添加一个条件OC=OD,使△COP≌△DOP(填一个即可).
如图,OP为∠AOB内的一条射线,PC⊥OA,PD⊥OB,垂足分别是C,D,请添加一个条件OC=OD,使△COP≌△DOP(填一个即可).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形AOBC的两条边OA,OB的长是方程x2-18x+80=0的两根,其中OA<OB,沿直线AD将矩形折叠,使点C与y轴上的点E重合.
如图,矩形AOBC的两条边OA,OB的长是方程x2-18x+80=0的两根,其中OA<OB,沿直线AD将矩形折叠,使点C与y轴上的点E重合.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
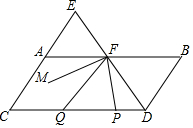 如图,点E在CA延长线上,DE、AB交于F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.则下列结论:
如图,点E在CA延长线上,DE、AB交于F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
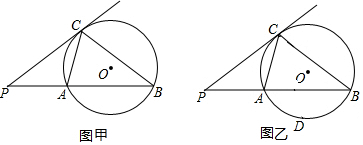
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
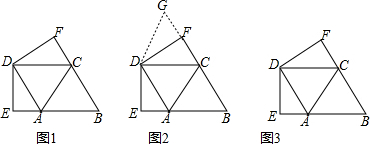
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com