
【题目】某服装厂里有许多剩余的三角形边角料,找出一块△ABC,测得∠C=90°(如图),现要从这块三角形上剪出一个半圆O,做成玩具,要求:使半圆O与三角形的两边AB、AC相切,切点分别为D、C,且与BC交于点E.
(1)在图中设计出符合要求的方案示意图.(要求:尺规作图,不写作法,保留作图痕迹).
(2)Rt△ABC中,AC=3,AB=5,连接AO,求出AO的长度.

【答案】(1)作图见解析;(2)AO为![]() .
.
【解析】
(1)以∠A的平分线与BC的交点为圆心,以到C的距离为半径的半圆即为所求;
(2)连接OD,在Rt△ABC中,根据勾股定理得BC=4,根据切线的性质和线段的和差关系得到BD=2,设⊙O的半径为r,则OB=4-r,根据勾股定理求得半径,再在Rt△ACO中,根据勾股定理求得AO.
(1) 半圆O就是所求的图形,
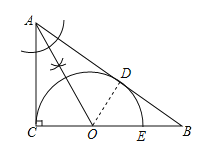
(2)连接OD,
∵Rt△ABC中,AC=3,AB=5,根据勾股定理得BC=4,
由题意可知,AB是⊙O的切线,
∴∠ODB=90°,AD=AC=3,
∴BD=2,
设⊙O的半径为r,则OB=4-r,
∴r2+22=(4-r)2.
解得![]() ,
,
在Rt△ACO中,根据勾股定理得![]() .
.


科目:初中数学 来源: 题型:
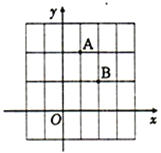
【题目】点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是![]() 轴上使得∣PA—PB∣的值最大的点,Q是
轴上使得∣PA—PB∣的值最大的点,Q是![]() 轴上使得QA+QB的值最小的点,则OP·OQ=__________.
轴上使得QA+QB的值最小的点,则OP·OQ=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作与探究:如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,折痕的一端G点在边BC上,BG=10.
①第一次折叠:当折痕的另一端点F在AB边上时,如图1,求折痕GF的长;
②第二次折叠:当折痕的另一端点F在AD边上时,如图2,证明四边形BGEF为菱形,并求出折痕GF的长.

(2)拓展延伸:通过操作探究发现在矩形纸片ABCD中,AB=5,AD=13.如图3所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ.当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则点A′在BC边上可移动的最大距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是x轴上使得![]() 的值最大的点,Q是y轴上使得QA十QB的值最小的点,则
的值最大的点,Q是y轴上使得QA十QB的值最小的点,则![]() = ▲ .
= ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
反比例函数y=![]() (k>0)第一象限内的图象如图1所示,点P、R是双曲线上不同的两点,过点P、R分别做PA⊥y轴于点A,RC⊥x轴于点C,两垂线交点为B.
(k>0)第一象限内的图象如图1所示,点P、R是双曲线上不同的两点,过点P、R分别做PA⊥y轴于点A,RC⊥x轴于点C,两垂线交点为B.
(1)问题提出:线段PB:PA与BR:RC有怎样的关系?
问题解决:设点PA=n,PB=m,则点P的坐标为(n,![]() ),点R的坐标为(m+n,
),点R的坐标为(m+n,![]() ),AO=BC=
),AO=BC=![]() ,RC=
,RC=![]() ,BR=
,BR=![]() ,
,
则BR:RC=![]() ,
,
PB:PA=![]() ,
,
∴PB:PA=BR:RC.
问题应用:
(2)利用上面的结论解决问题:
①如图1,如果BR=6,CR=3,AP=4,BP= .
②如图2,如果直线PR的关系式y2=﹣x+3,与x轴交于点D,与y轴交于点E,若ED=3PR,求出k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,折叠长方形(四个角都是直角)的一边AD使点D落在BC边的点F处,已知AB=DC=8cm,AD=BC=10cm,

求:(1)求BF长度;
(2)求CE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线一点,点O是线段AD上一点,OP=OC.
(1)已知∠APO=18°,求∠DCO的度数;
(2)求证:△OPC是等边三角形;
(3)求证:AC=AO+AP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=![]() x +m和y=-
x +m和y=-![]() x +n的图象都是经过点A(-2,0),且与y轴分别交于B、C两点.
x +n的图象都是经过点A(-2,0),且与y轴分别交于B、C两点.
(1)直接写出B、C两点的坐标B: ;C:
(2)求ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com